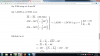
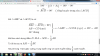
Ta chứng minh điều đó theo cách sau :

Lấy D" role="presentation" style="display: inline-block; line-height: 0; font-size: 16.38px; word-wrap: normal; word-spacing: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; margin: 0px; padding: 1px 0px; position: relative;">DD đối xứng với A" role="presentation" style="display: inline-block; line-height: 0; font-size: 16.38px; word-wrap: normal; word-spacing: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; margin: 0px; padding: 1px 0px; position: relative;">AA qua M" role="presentation" style="display: inline-block; line-height: 0; font-size: 16.38px; word-wrap: normal; word-spacing: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; margin: 0px; padding: 1px 0px; position: relative;">MM.
Xét △ABM" role="presentation" style="display: inline-block; line-height: 0; font-size: 16.38px; word-wrap: normal; word-spacing: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; margin: 0px; padding: 1px 0px; position: relative;">△ABM△ABM và △CDM" role="presentation" style="display: inline-block; line-height: 0; font-size: 16.38px; word-wrap: normal; word-spacing: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; margin: 0px; padding: 1px 0px; position: relative;">△CDM△CDM, ta có:
M1^=M2^(đối đỉnh)MB=MC(=12BC)MA=MD(=12AD)}⇒△ABM=△DCM (c.g.c)⇒{AB=CDA1^=D1^" role="presentation" style="display: inline-block; line-height: 0; font-size: 16.38px; word-wrap: normal; word-spacing: normal; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; margin: 0px; padding: 1px 0px; position: relative;">ˆM1=ˆM2(đối đỉnh)MB=MC(=12BC)MA=MD(=12AD)⎫⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎬⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎭⇒△ABM=△DCM (c.g.c)⇒{AB=CDˆA1=ˆD1M1^=M2^(đối đỉnh)MB=MC(=12BC)MA=MD(=12AD)}⇒△ABM=△DCM (c.g.c)⇒{AB=CDA1^=D1^
Mặt khác, ta có:
A1^+A2^=BAC^=90∘⇔ D1^+A2^=90∘⇔ 180∘−(D1^+A2^

=180∘−90∘⇔ ACD^=90∘( tổng ba góc trong của △ACD)" role="presentation" style="display: inline-block; line-height: 0; font-size: 16.38px; word-wrap: normal; word-spacing: normal; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; margin: 0px; padding: 1px 0px; position: relative;">ˆA1+ˆA2=ˆBAC=90∘⇔ ˆD1+ˆA2=90∘⇔ 180∘−(ˆD1+ˆA2)=180∘−90∘⇔ ˆACD=90∘( tổng ba góc trong của △ACD)A1^+A2^=BAC^=90∘⇔ D1^+A2^=90∘⇔ 180∘−(D1^+A2^)=180∘−90∘⇔ ACD^=90∘( tổng ba góc trong của △ACD)
Xét △ABC" role="presentation" style="display: inline-block; line-height: 0; font-size: 16.38px; word-wrap: normal; word-spacing: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; margin: 0px; padding: 1px 0px; position: relative;">△ABC△ABC và △ACD" role="presentation" style="display: inline-block; line-height: 0; font-size: 16.38px; word-wrap: normal; word-spacing: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; margin: 0px; padding: 1px 0px; position: relative;">△ACD△ACD, ta có:
BAC^=ACD^(=90∘

AB=CD(cmt)AC chung}⇒△ABC=△CDA (c.g.c)⇒BC=AD" role="presentation" style="display: inline-block; line-height: 0; font-size: 16.38px; word-wrap: normal; word-spacing: normal; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; margin: 0px; padding: 1px 0px; position: relative;">ˆBAC=ˆACD(=90∘)AB=CD(cmt)AC chung⎫⎪ ⎪⎬⎪ ⎪⎭⇒△ABC=△CDA (c.g.c)⇒BC=ADBAC^=ACD^(=90∘)AB=CD(cmt)AC chung}⇒△ABC=△CDA (c.g.c)⇒BC=AD
Mà theo cách dựng điểm D" role="presentation" style="display: inline-block; line-height: 0; font-size: 16.38px; word-wrap: normal; word-spacing: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; margin: 0px; padding: 1px 0px; position: relative;">DD: MA=MD=12AD" role="presentation" style="display: inline-block; line-height: 0; font-size: 16.38px; word-wrap: normal; word-spacing: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; margin: 0px; padding: 1px 0px; position: relative;">MA=MD=12ADMA=MD=12AD
Từ đó ta suy ra AM=12BC" role="presentation" style="display: inline-block; line-height: 0; font-size: 16.38px; word-wrap: normal; word-spacing: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; margin: 0px; padding: 1px 0px; position: relative;">AM=12BCAM=12BC
Hay là trong 1 tam giác vuông, trung tuyến ứng với cạnh huyền bằng 12" role="presentation" style="display: inline-block; line-height: 0; font-size: 16.38px; word-wrap: normal; word-spacing: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; margin: 0px; padding: 1px 0px; position: relative;">1212 cạnh huyền.
Chứng minh hoàn tất tại đây. (◼

" role="presentation" style="display: inline-block; line-height: 0; font-size: 16.38px; word-wrap: normal; word-spacing: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; margin: 0px; padding: 1px 0px; position: relative;">(■)
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.