- 9 Tháng sáu 2017
- 1,687
- 1,785
- 284
- Điện Biên
- ♦ Tiên học lễ _ Hậu học văn _ Đập đá quay tay ♦ ( ♥ cần chút sức lực ♥)
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
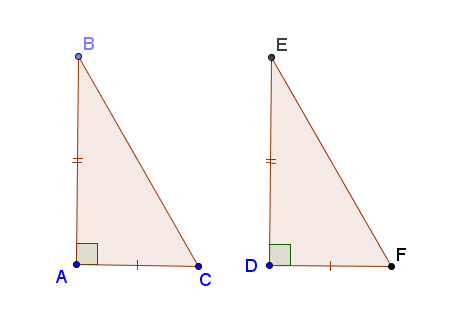
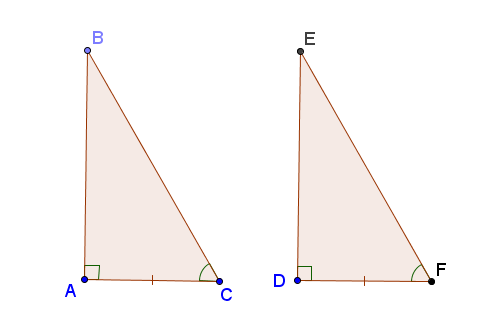
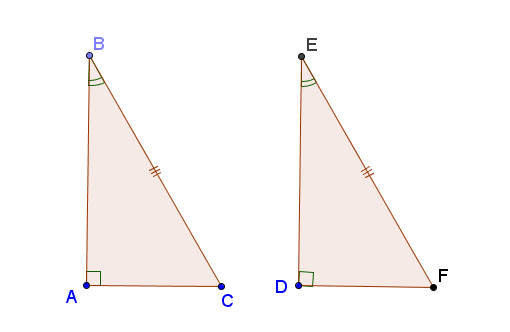
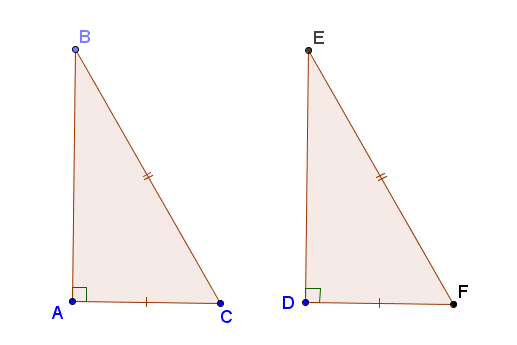
* Nêu các trường hợp bằng nhau của tm giác và tam giá vuông
* Cho tam giác ABC cân tại A, BH vuông góc với AC tại H. Trên cạnh BC lấy điểm M bất kì (Khác B,C).Gọi D,E,F là chân đường vuông góc hạ từ M đến AB,AC,BH. Hãy chứng minh rằng tam giác DBM và tam giác FMB
* Cho tam giác ABC cân tại A, BH vuông góc với AC tại H. Trên cạnh BC lấy điểm M bất kì (Khác B,C).Gọi D,E,F là chân đường vuông góc hạ từ M đến AB,AC,BH. Hãy chứng minh rằng tam giác DBM và tam giác FMB