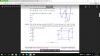
từ M kẻ // NP cắt DD' tại Q => thiết diện NMQP
từ N kẻ // BC, AB cắt AA' tại E, CC' tại K
từ E kẻ // AD cắt DD' tại F
=> [tex]V_{ABCD.MNPQ}=V_{ABCD.EFKN}+V_{N.EFQM}+V_{N.FKPQ}[/tex]
từ M kẻ // AD cắt DD' tại H
Vì MQ// NP
=> tam giác NKP = MHQ
=> HQ = KP => FQ = CP
AD =a, AB= b, AA' = c
[tex]V_{N.EFQM} =\frac{1}{3}EN.\frac{(ME+FQ)EF}{2}=\frac{1}{6}.b.(\frac{c}{4}+\frac{c}{3}).a=\frac{7}{72}abc[/tex]
[tex]V_{N.FKPQ}=\frac{1}{3}NK.\frac{(FQ+KP)FK}{2}=\frac{1}{6}.a.(\frac{c}{3}+\frac{c}{3}-\frac{c}{4}).b=\frac{5}{72}abc[/tex]
[tex]V_{ABCD.EFKN}=AB.AD.AE=a.b.\frac{c}{4}=\frac{1}{4}abc[/tex]
=> [tex]V_{ABCD.MNPQ}=\frac{5}{12}abc=\frac{5275}{6}[/tex]
=> [tex]V_{MNPQ.A'B'C'D'}=\frac{7385}{6}[/tex]
vì lấy phần nhỏ hơn => chọn D
biết là cách này dài cơ mà ra còn hơn k bạn thông cảm.
Good luck
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
