Một bàn có 4 chân.Nếu đặt 1 vật có trọng lượng lớn hơn 2P thì chân bàn gãy.Hãy tìm quỹ tích các điểm sao cho chân bàn không gãy với 1 vật trọng lượng p.
Giúp mình với
Đặt vật trọng lượng 2P thì chân bàn gẫy nên mỗi chân bàn chịu một lực tối đa
[TEX]F_{max}=\frac{2P}{4}=\frac{P}{2}[/TEX]
Ta xét vị trí để chân bàn 1 không gẫy khi đặt vật
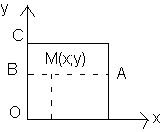
Chọn gốc toạ độ như hình vẽ, chân bàn 1 là tâm 0, chân bàn 2 là điểm C, 2 chân bàn còn lại lần lượt là 2 đỉnh của hình vuông
M là điểm đặt vật
Vật gây ra các lực 1,2,3,4 lên 4 chân bàn
Trước hết, ta phân tích P theo phương AB
[TEX]\frac{F_A}{F_B}=\frac{MB}{MA}=\frac{x}{a-x} \Rightarrow \frac{F_B}{P}=\frac{a-x}{a}[/TEX]
Phân tích tiếp F_B theo phương OC
[TEX]\frac{F_2}{F_1}=\frac{BO}{BC}=\frac{y}{a-y} \Rightarrow \frac{F_1}{F_B}=\frac{a-y}{a}[/TEX]
[TEX]\Rightarrow F_1=P\frac{(a-x)(a-y)}{a^2}[/TEX]
Để chân bàn không gẫy
[TEX]F_1 \leq F_{max} \Leftrightarrow \frac{(a-x)(a-y)}{a^2} \leq \frac{1}{2} \Rightarrow y \geq a-\frac{a^2}{2(a-x)}[/TEX]
Đường giới hạn này là 1 hyperbol đi qua trung điểm 2 cạnh
Đối với các chân bàn khác, giải tương tự
\Rightarrow Các điểm có thể đặt vật là phần giới hạn bởi 4 cung hyperbol đi qua trung điểm của 4 cạnh
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
