Bạn muốn xét 1 vật có DĐĐH không thì xét li độ của nó có phải là một hàm cosin hoặc sin theo thời gian không nhé (định nghĩa SGK: Dao động điều hòa là dao động trong đó li độ của vật là một hàm côsin (hay sin) của thời gian).
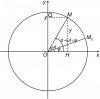
Trên hình vẽ thì điểm [tex]M[/tex] chuyển động tròn đều với vận tốc góc [tex]\omega[/tex] không đổi, vị trí ban đầu tại [tex]M_0[/tex] với góc quay [tex]\varphi[/tex], do đó góc quay của điểm [tex]M[/tex] tại thời điểm [tex]t[/tex] so với trục Ox dễ thấy là [tex]\alpha =\omega t+\varphi[/tex]. Nếu [tex]Q[/tex] là hình chiếu của [tex]M[/tex] lên trục Oy thì li độ [tex]y[/tex] của điểm [tex]Q[/tex] được tính là: [tex]y=\sin\alpha =\sin(\omega t + \varphi)[/tex] là một hàm điều hòa theo thời gian nên điểm [tex]Q[/tex] DĐĐH trên trục Oy. Done.
Tới đây mình muốn nói thêm 1 chút nữa. Một vật chuyển động tròn đều thì hình chiếu của nó lên một đường thẳng bất kỳ trong mặt phẳng quỹ đạo thì đều cho một DĐĐH trên đường thẳng đó. SGK trước đây sử dụng hình chiếu của [tex]M[/tex] lên trục Oy như hình trên và định nghĩa mặc định là [tex]x=\sin(\omega t + \varphi)[/tex] (1) (họ đổi chữ [tex]y[/tex] thành chữ [tex]x[/tex], định nghĩa mà, thích dùng chữ gì thì dùng thôi), còn SGK hiện nay sử dụng hình chiếu của [tex]M[/tex] lên trục Ox và định nghĩa mặc định như chúng ta học hiện nay là [tex]x=\cos(\omega t + \varphi)[/tex] (2). Dĩ nhiên cả 2 đều đúng, mỗi cái có ưu khuyết riêng, nếu sử dụng (1) thì khi đạo hàm ra vận tốc có dạng [tex]v=\omega\cos(\omega t + \varphi)[/tex] rất đẹp, còn sử dụng (2) thì [tex]v=-\omega\sin(\omega t + \varphi)[/tex] có dấu "-" mất đẹp; tuy nhiên định nghĩa (2) thì cho hình ảnh xuống trục Ox dễ nhìn hơn, cá nhân mình thích cách định nghĩa hiện nay hơn.
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
