a)
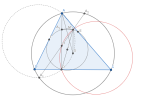
Ta sẽ định nghĩa lại điểm [imath]M[/imath] là giao điểm của đường thẳng vuông góc với [imath]BC[/imath] qua [imath]O[/imath] với đường tròn Euler của [imath]\Delta ABC[/imath] sao cho [imath]M \notin BC[/imath].
Gọi [imath]A_3[/imath] là trung điểm của [imath]AH[/imath] thì [imath]A_3[/imath] thuộc đường tròn Euler của [imath]\Delta ABC[/imath].
Xét phép vị tự [imath]\mathcal{V}[/imath] tâm [imath]H[/imath] tỉ số [imath]k=2[/imath] biến đường tròn Euler thành [imath](O)[/imath]
Lấy [imath]A_2[/imath] là ảnh của [imath]M[/imath] qua [imath]\mathcal{V}[/imath] thì [imath]A_2 \in (O)[/imath] và [imath]HM=MA_2[/imath]
Ta có [imath]A_3M \parallel AA_2 \Rightarrow AA_2 \parallel BC[/imath]
Lấy [imath]A_1[/imath] là giao điểm khác [imath]A_2[/imath] của [imath]A_2H[/imath] với [imath](O)[/imath]. Khi đó phép nghịch đảo [imath]\mathcal{I}[/imath] tâm [imath]H[/imath] phương tích [imath]\overline{HA}\overline{HD}[/imath] biến đường tròn Euler thành [imath](O)[/imath] nên [imath]A_1[/imath] là ảnh của [imath]M[/imath] qua [imath]\mathcal{I}[/imath]
Từ đó [imath]AA_1DM[/imath] nội tiếp nên [imath]\widehat{ADM}=\widehat{AA_1M}=\widehat{AA_1A_2}[/imath]
Mà [imath]MO \perp AA_2 \Rightarrow \widehat{AA_1A_2}=\widehat{AOM} \Rightarrow \widehat{AOM}=\widehat{ADM} \Rightarrow ADOM[/imath] nội tiếp
Suy ra [imath]M[/imath] là giao điểm của [imath](DEF)[/imath] và [imath](AOD)[/imath].
Nhận thấy [imath]OA=OA_1 \Rightarrow \widehat{OAA_1}=\widehat{OA_1A}[/imath]
Mà [imath]AD \parallel OM \Rightarrow \widehat{OAD}=\widehat{AA_1M} \Rightarrow \widehat{A_1AD}=\widehat{OA_1M}=\widehat{OAM}[/imath]
Lại có [imath]AO,AD[/imath] đẳng giác trong [imath]\widehat{BAC}[/imath] nên [imath]AA_1,AM[/imath] đẳng giác trong [imath]\widehat{BAC}[/imath]
Từ đó thay vì chứng minh [imath]AM,BN,CP[/imath] đồng quy ta chứng minh [imath]AA_1,BB_1,CC_1[/imath]
Qua [imath]\mathcal{I}[/imath] ta có [imath]AA_1 \leftrightarrow (HDM), BB_1 \leftrightarrow (HEN), CC_1 \leftrightarrow (HFP)[/imath] nên ta cần chứng minh [imath](HDM),(HEN),(HFP)[/imath] đồng trục.
Nhận thấy [imath]\widehat{DA_3M}=90^o[/imath] nên tâm [imath]I[/imath] của đường tròn Euler là trung điểm [imath]MD[/imath]. Từ đó [imath]\mathcal{P}_{I \setminus (HDM)}=ID^2[/imath]
Tương tự [imath]\mathcal{P}_{I \setminus (HEN)}=IE^2,\mathcal{P}_{I \setminus (HFP)}=IF^2[/imath] nên [imath]\mathcal{P}_{I \setminus (HDM)}=\mathcal{P}_{I \setminus (HEN)}=\mathcal{P}_{I \setminus (HFP)}[/imath] hay [imath]I[/imath] có cùng phương tích với [imath]3[/imath] đường tròn [imath](HDM),(HEN),(HFP)[/imath].
Suy ra [imath](HDM),(HEN),(HFP)[/imath] đồng trục [imath]HI[/imath]. Ta có đpcm.
b)
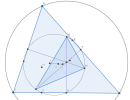
Gọi [imath]X,Y,Z[/imath] là trung điểm [imath]BC,CA,AB[/imath] thì ta thấy [imath]X,O,M[/imath] thẳng hàng, [imath]Y,O,N[/imath] thẳng hàng và [imath]Z,O,P[/imath] thẳng hàng.
Ta có [imath]\widehat{ZNM}=\widehat{ZXM}=90^o-\widehat{BXZ}=90^o-\widehat{C}[/imath]
[imath]\widehat{ZNP}=\widehat{ZYP}=90^o-\widehat{AYZ}=90^o-\widehat{C} \Rightarrow \widehat{ZNM}=\widehat{ZNP}[/imath]
Suy ra [imath]NZ[/imath] là phân giác của [imath]\widehat{MNP}[/imath]. Tương tự thì [imath]MX,PY[/imath] cũng là các đường phân giác của [imath]\Delta MNP[/imath]
[imath]\Rightarrow O[/imath] là tâm nội tiếp của [imath]\Delta MNP[/imath].
Xét phép vị tự [imath]\mathcal{V}[/imath] tâm [imath]G[/imath] là trọng tâm [imath]\Delta ABC[/imath], tỉ số [imath]k=-\dfrac{1}{2}[/imath]
Ảnh của [imath]A,B,C,H[/imath] qua [imath]\mathcal{V}[/imath] lần lượt là [imath]X,Y,Z,O[/imath].
Gọi [imath]L'[/imath] là ảnh của [imath]L[/imath] qua [imath]\mathcal{V}[/imath] thì [imath]HL \parallel L'O[/imath]. Từ đó ta cần chứng minh [imath]L',O,K[/imath] thẳng hàng.
Xét bài toán mô hình [imath]\Delta MNP[/imath] có tâm nội tiếp [imath]O[/imath], [imath]MO,NO,PO[/imath] cắt đường tròn [imath](MNP)[/imath] lần lượt tại [imath]X,Y,Z[/imath]. Gọi [imath]L',K[/imath] là điểm Lemoine của [imath]\Delta MNP[/imath] và [imath]\Delta XYZ[/imath] thì [imath]L'O,K[/imath] thẳng hàng.
Ta đưa về cấu hình tổng quát hơn 1 chút:
"Cho [imath]\Delta ABC[/imath] nhọn và điểm [imath]I[/imath] bất kỳ trong tam giác. [imath]AI,BI,CI[/imath] cắt [imath](ABC)[/imath] tại [imath]D,E,F[/imath]. Gọi [imath]L,L'[/imath] là tâm Lemoine của [imath]\Delta ABC, \Delta DEF[/imath] thì [imath]L,I,L'[/imath] thẳng hàng."
Nhận xét: Nếu ta gọi [imath]A_1,D_1[/imath] là giao điểm của [imath]AL[/imath] và [imath]DL'[/imath] với [imath](ABC)[/imath] thì [imath]A_1,I,D_1[/imath] thẳng hàng.
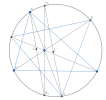
Thật vậy, ta định nghĩa lại điểm [imath]D_1[/imath] là giao điểm [imath]IA_1[/imath] với [imath](ABC)[/imath]. Ta cần chứng minh [imath]DFD_1E[/imath] là tứ giác điều hòa.
Ta có [imath]ABA_1C[/imath] là tứ giác điều hòa nên [imath]\dfrac{BA}{BA_1}=\dfrac{CA}{CA_1}[/imath]
Lại có: [imath]\dfrac{A_1B}{D_1E}=\dfrac{IB}{ID_1},\dfrac{AB}{DE}=\dfrac{IB}{ID}[/imath]
[imath]\Rightarrow \dfrac{AB}{A_1B}=\dfrac{AB}{DE}\cdot \dfrac{D_1E}{A_1B}\cdot \dfrac{DE}{D_1E}=\dfrac{IB}{ID} \cdot \dfrac{ID_1}{IB} \cdot {DE}{D_1E}[/imath]
[imath]=\dfrac{ID_1}{ID} \cdot \dfrac{ED_1}{ED}[/imath]
Tương tự thì [imath]\dfrac{AC}{A_1C}=\dfrac{ID_1}{ID} \cdot \dfrac{FD_1}{FD}[/imath]
[imath]\Rightarrow \dfrac{ED_1}{ED}=\dfrac{FD_1}{FD}[/imath] hay [imath]DFD_1E[/imath] là tứ giác điều hòa.
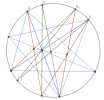
Tới đây gọi tiếp [imath]B_1,E_1[/imath] là giao điểm của [imath]BL,EL'[/imath] với [imath](ABC)[/imath], [imath]G[/imath] là giao điểm của [imath]DB_1[/imath] và [imath]EA_1[/imath].
Áp dụng định lý Pascal cho bộ điểm [imath]\begin{pmatrix} A & B_1 & E \\ B & A_1 & D \end{pmatrix}[/imath] ta được [imath]L,I,G[/imath] thẳng hàng.
Áp dụng định lý Pascal cho bộ điểm [imath]\begin{pmatrix} D & B_1 & E \\ E_1 & A_1 & D \end{pmatrix}[/imath] ta được [imath]L',I,G[/imath] thẳng hàng.
Vậy ta có điều phải chứng minh.
Nếu còn thắc mắc chỗ nào bạn hãy trả lời dưới topic này để được hỗ trợ nhé ^^ Chúc bạn học tốt ^^
Ngoài ra, bạn tham khảo kiến thức tại đây nhé
[Chuyên đề HSGQG] Định lý LTE, cấp của số nguyên và phương trình nghiệm nguyên chứa lũy thừa
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
