L
lightning.shilf_bt
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
* xét với dao động nhỏ của con lắc đơn [TEX]\alpha_o[/TEX]\leq[TEX]10^o[/TEX]
khi đó thế năng được tính theo công thức [TEX]E_t[/TEX]=mgh=[TEX]mgl(1-cos\alpha)=\frac{mgl.\alpha^2}{2}=\frac{mg.S^2}{2l}=\frac{m.\omega^2.S^2}{2}[/TEX]
cơ năng : E=[TEX]E_t[/TEX] + Eđ =[TEX]mgl.(1-cos\alpha_o)=\frac{mgl.\alpha_o^2}{2}=\frac{mg.S_o^2}{2l}=const [/TEX]
lưu ý : cơ năng là đại lượng bảo toàn , cơ năng không bao giờ mất đi mà nó chỉ chuyển đổi sang 1 dạng năng lượng khác .
với [TEX]\alpha_o[/TEX] << thì bỏ qua ma sát \Rightarrow con lắc đơn gia động điều hòa với [TEX]\omega[/TEX] , T, f thì [TEX]E_t[/TEX] và Eđ biến thiên tuần hoàn với [tex]\left[\begin{\omega_1=2.\omega}\\{f_1=2.f}\\{T_1=\frac{T}{2}} [/tex]
* [TEX]E_t[/TEX] và Eđ biến thiên tuần hoàn cùng tần số nhưng ngược pha nhau , chúng có thể chuyển hoa cho nhau nhưng tổng cơ năng dc bảo toàn và tỉ lệ thuận với bình phương biên độ dao động [TEX]A^2[/TEX]
tại 1 thời điểm t bất kì thì [TEX]E_t[/TEX] và Eđ có giá trị nào đó thì thời điểm chúng lặp lại như cũ là t'=t+[TEX]\frac{n.T}{2}[/TEX] trong đó n thuộc N
trong 1 chu kì thì có 4 thời điểm [TEX]E_t[/TEX]=Eđ tại vị trí vật có li độ là x=[TEX]\pm \frac{A}{\sqrt{2}}[/TEX] , cứ sau nhưng khoảng thời gian t= [TEX]\frac{T}{4}[/TEX] thì [TEX]E_t[/TEX]=Eđ=[TEX]\frac{E}{2}[/TEX]
- thời gian ngắn nhất để vật đi từ x=0 đến x=[TEX]\pm[/TEX] A hoặc ngược lại là t=[TEX]\frac{T}{4}[/TEX]
-thời gian ngắn nhất để vật đi từ x=0 đến x=[TEX]\pm[/TEX][TEX]\frac{A}{2}[/TEX] hoặc ngược lại là t = [TEX]\frac{T}{12}[/TEX]
- thời gian ngắn nhất để vật đi từ x=[TEX]\frac{A}{2}[/TEX] đến x=a hoặc ngược lại là t =[TEX]\frac{T}{6}[/TEX]
- thời gian ngắn nhất để vật đi từ x=0 đến x=[TEX]\pm[/TEX] [TEX]\frac{A}{\sqrt{2}}[/TEX] hoặc ngược lại là t=[TEX]\frac{T}{8}[/TEX]
-thời gian ngắn nhất để vật đi từ x=[TEX]\pm[/TEX] [TEX]\frac{A}{\sqrt{2}}[/TEX] đến x= A hoặc ngược lại là t= [TEX]\frac{T}{8}[/TEX]
- thời gian vật đi từ x=0 đến x=[TEX]\pm[/TEX] [TEX]\frac{A.\sqrt{3}}{2}[/TEX] hoặc ngược lại là t= [TEX]\frac{T}{6}[/TEX]
- thời gian ngắn nhất để vật đi từ x=[TEX]\frac{A.\sqrt{3}}{2}[/TEX] đến x=A hoặc ngược lại là t= [TEX]\frac{T}{12}[/TEX]
* động năng
Eđ = E - [TEX]E_t[/TEX]=[TEX]\frac{mg}{2.l}.(S_o^2-S^2}=\frac{mgl}{2}.(\alpha_o^2-\alpha^2)[/TEX]
nếu [TEX]\alpha[/TEX] =[TEX]\pm\frac{\alpha_o}{n}[/TEX] hoặc S=[TEX]\pm\frac{S_o}{n}[/TEX] thì [TEX]E_t[/TEX]=[TEX]\frac{E}{n^2}[/TEX] \Rightarrow Eđ=[TEX]\frac{n^2-1}{n^2}[/TEX].E
ví dụ cho biết [TEX]E_t[/TEX]=Eđ
thì [tex]\left[\begin{\alpha=\pm \frac{\alpha_o}{\sqrt{2}}}\\{S=\pm \frac{S_o}{\sqrt{2}}\\{V=\pm \frac{V_{max}}{\sqrt{2}} [/tex]
* một cách tổng quát nếu Eđ=n.[TEX]E_t[/TEX] suy ra E=(n+1).[TEX]E_t[/TEX]
suy ra [TEX]\left[\begin{E_t=\frac{E}{n+1}}\\{Eđ=\frac{n.E}{n+1}} [/TEX] \Rightarrow [tex]\left[\begin{\alpha=\pm \frac{\alpha_o}{\sqrt{n+1}}\\{S=\pm \frac{S_o}{\sqrt{n+1}}}\\{V= \pm V_{max}.\sqrt{\frac{n}{n+1}}} [/tex]
****
tính biên độ góc ở 2 bên VTCB khi con lắc vướng đinh]
hình vẽ
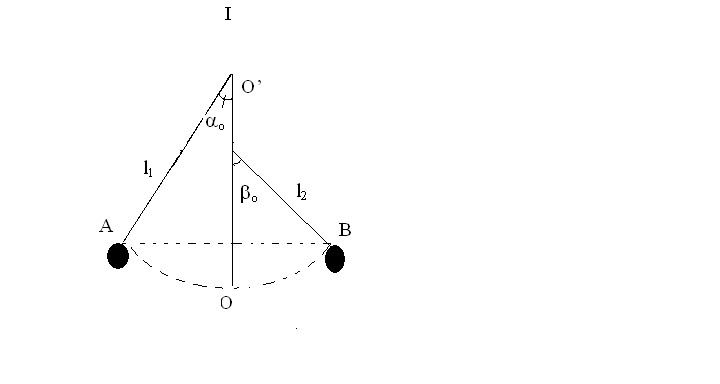
* con lắc bị vướng đinh tại điểm I nằm trên đường thẳng đứng OO'
ta luôn có [TEX]l_2=l_1-IO'[/TEX]
áp dụng đinh luật bảo toàn cơ năng ta có [TEX]E_A=E_B[/TEX]
[TEX]\alpha_o , \beta_o[/TEX] \leq [TEX]10^o[/TEX]
\Leftrightarrow [TEX]\frac{mg.l_1.\alpha_o^2}{2}=\frac{mg.l_2.\beta_o^2}{2}[/TEX] \Leftrightarrow [TEX]\frac{\alpha_o}{\beta_o}=\sqrt{\frac{l_2}{l_1}}[/TEX]
lực căng ở 2 biên
[TEX]\frac{T_A}{T_B}=\frac{cos\alpha_o}{cos\beta_o}[/TEX]
chúc các bạn học tốt
khi đó thế năng được tính theo công thức [TEX]E_t[/TEX]=mgh=[TEX]mgl(1-cos\alpha)=\frac{mgl.\alpha^2}{2}=\frac{mg.S^2}{2l}=\frac{m.\omega^2.S^2}{2}[/TEX]
cơ năng : E=[TEX]E_t[/TEX] + Eđ =[TEX]mgl.(1-cos\alpha_o)=\frac{mgl.\alpha_o^2}{2}=\frac{mg.S_o^2}{2l}=const [/TEX]
lưu ý : cơ năng là đại lượng bảo toàn , cơ năng không bao giờ mất đi mà nó chỉ chuyển đổi sang 1 dạng năng lượng khác .
với [TEX]\alpha_o[/TEX] << thì bỏ qua ma sát \Rightarrow con lắc đơn gia động điều hòa với [TEX]\omega[/TEX] , T, f thì [TEX]E_t[/TEX] và Eđ biến thiên tuần hoàn với [tex]\left[\begin{\omega_1=2.\omega}\\{f_1=2.f}\\{T_1=\frac{T}{2}} [/tex]
* [TEX]E_t[/TEX] và Eđ biến thiên tuần hoàn cùng tần số nhưng ngược pha nhau , chúng có thể chuyển hoa cho nhau nhưng tổng cơ năng dc bảo toàn và tỉ lệ thuận với bình phương biên độ dao động [TEX]A^2[/TEX]
tại 1 thời điểm t bất kì thì [TEX]E_t[/TEX] và Eđ có giá trị nào đó thì thời điểm chúng lặp lại như cũ là t'=t+[TEX]\frac{n.T}{2}[/TEX] trong đó n thuộc N
trong 1 chu kì thì có 4 thời điểm [TEX]E_t[/TEX]=Eđ tại vị trí vật có li độ là x=[TEX]\pm \frac{A}{\sqrt{2}}[/TEX] , cứ sau nhưng khoảng thời gian t= [TEX]\frac{T}{4}[/TEX] thì [TEX]E_t[/TEX]=Eđ=[TEX]\frac{E}{2}[/TEX]
- thời gian ngắn nhất để vật đi từ x=0 đến x=[TEX]\pm[/TEX] A hoặc ngược lại là t=[TEX]\frac{T}{4}[/TEX]
-thời gian ngắn nhất để vật đi từ x=0 đến x=[TEX]\pm[/TEX][TEX]\frac{A}{2}[/TEX] hoặc ngược lại là t = [TEX]\frac{T}{12}[/TEX]
- thời gian ngắn nhất để vật đi từ x=[TEX]\frac{A}{2}[/TEX] đến x=a hoặc ngược lại là t =[TEX]\frac{T}{6}[/TEX]
- thời gian ngắn nhất để vật đi từ x=0 đến x=[TEX]\pm[/TEX] [TEX]\frac{A}{\sqrt{2}}[/TEX] hoặc ngược lại là t=[TEX]\frac{T}{8}[/TEX]
-thời gian ngắn nhất để vật đi từ x=[TEX]\pm[/TEX] [TEX]\frac{A}{\sqrt{2}}[/TEX] đến x= A hoặc ngược lại là t= [TEX]\frac{T}{8}[/TEX]
- thời gian vật đi từ x=0 đến x=[TEX]\pm[/TEX] [TEX]\frac{A.\sqrt{3}}{2}[/TEX] hoặc ngược lại là t= [TEX]\frac{T}{6}[/TEX]
- thời gian ngắn nhất để vật đi từ x=[TEX]\frac{A.\sqrt{3}}{2}[/TEX] đến x=A hoặc ngược lại là t= [TEX]\frac{T}{12}[/TEX]
* động năng
Eđ = E - [TEX]E_t[/TEX]=[TEX]\frac{mg}{2.l}.(S_o^2-S^2}=\frac{mgl}{2}.(\alpha_o^2-\alpha^2)[/TEX]
nếu [TEX]\alpha[/TEX] =[TEX]\pm\frac{\alpha_o}{n}[/TEX] hoặc S=[TEX]\pm\frac{S_o}{n}[/TEX] thì [TEX]E_t[/TEX]=[TEX]\frac{E}{n^2}[/TEX] \Rightarrow Eđ=[TEX]\frac{n^2-1}{n^2}[/TEX].E
ví dụ cho biết [TEX]E_t[/TEX]=Eđ
thì [tex]\left[\begin{\alpha=\pm \frac{\alpha_o}{\sqrt{2}}}\\{S=\pm \frac{S_o}{\sqrt{2}}\\{V=\pm \frac{V_{max}}{\sqrt{2}} [/tex]
* một cách tổng quát nếu Eđ=n.[TEX]E_t[/TEX] suy ra E=(n+1).[TEX]E_t[/TEX]
suy ra [TEX]\left[\begin{E_t=\frac{E}{n+1}}\\{Eđ=\frac{n.E}{n+1}} [/TEX] \Rightarrow [tex]\left[\begin{\alpha=\pm \frac{\alpha_o}{\sqrt{n+1}}\\{S=\pm \frac{S_o}{\sqrt{n+1}}}\\{V= \pm V_{max}.\sqrt{\frac{n}{n+1}}} [/tex]
****
tính biên độ góc ở 2 bên VTCB khi con lắc vướng đinh]
hình vẽ
* con lắc bị vướng đinh tại điểm I nằm trên đường thẳng đứng OO'
ta luôn có [TEX]l_2=l_1-IO'[/TEX]
áp dụng đinh luật bảo toàn cơ năng ta có [TEX]E_A=E_B[/TEX]
[TEX]\alpha_o , \beta_o[/TEX] \leq [TEX]10^o[/TEX]
\Leftrightarrow [TEX]\frac{mg.l_1.\alpha_o^2}{2}=\frac{mg.l_2.\beta_o^2}{2}[/TEX] \Leftrightarrow [TEX]\frac{\alpha_o}{\beta_o}=\sqrt{\frac{l_2}{l_1}}[/TEX]
lực căng ở 2 biên
[TEX]\frac{T_A}{T_B}=\frac{cos\alpha_o}{cos\beta_o}[/TEX]
chúc các bạn học tốt
Last edited by a moderator: