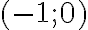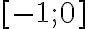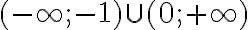kiem tra 15 phut

[dinhthoi0905]

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

Cho hàm số

. Tập xác định của hàm số là R thì m thuộc khoảng nào sau đây:

• 
• 
• 
• 

co ai biet cach lam bai nay khong, tui bo tay roi`

 

[vipbosspro]

hàm só


log cơ số a của b thì đk tồn tại trên R là a>0 b>0 và b #1
vậy thì:
điều kiện là x2 +2mx-m>0
x2 >m(1-2x)
khi 1-2x >0 \Leftrightarrowx<1/2 thì m<x21-2x)
khi 1-2x <0\Leftrightarrowx>1/2 thì m>x21-2x)
khi 1-2x=0\Leftrightarrowx=1/2 luôn thoả mãn x2+2mx-m>0 với \forallm
xét hàm y=f(x)=x2 1-2x) trên R\[1/2]
rồi sau đó tìm ra các khoảng max min của hàm số trên tập xác định
để m<x2/(1-2x) với \forallx<1/2 thì m<Minf(x)
để m>x2/(1-2x)với \forallx>1/2 thì m>Maxf(x)
và cuối cùng kết luận
thế nhé có ji thắc mắc thì cứ reply

 

[vipbosspro]

sửa tí

>-
éc tớ nhầm tí nhé
mấy cái hiểu tượng ý mà do ko để ý nên kho post lên bị lỗi
những cái đó tương đương với dấu hai chấm và dấu ngoặc mở tức là : và (
hehe