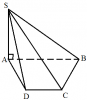
Cho hình chóp S.ABCD có đáy ABCD là nửa lục giác đều nội tiếp đường tròn đường kính AB = 2a, SA [tex]\perp[/tex] (ABCD) và SA = a
a. Tính d(AB, (SCD))
b. Một mặt phẳng [tex](\alpha )[/tex] song song với (SAD) cách (SAD) một khoảng bằng [tex]\frac{a\sqrt{3}}{4}[/tex]. Tính diện tích thiết diện mà [tex](\alpha )[/tex] cắt hình chóp S.ABCD.
View attachment 173949
a) $ABCD$ là đáy nửa lục giác đều nên $AB//CD=> AB//(SCD)$.
$d(AB,(SCD))=d(A,(SDC))$.
Trong mp' $(ABCD)$, từ $A$ kẻ $AH \perp CD$ tại $H$.
Ta có: [tex]\left\{\begin{matrix} SA \perp CD & \\ AH \perp CD & \\ SA \cap AH=A& \end{matrix}\right.=> CD \perp (SAH)=> (SAH)\perp(SDC)[/tex].
Từ $A$ kẻ $AI \perp SH=> AI \perp (SDC)=> d(A,(SDC))=AI$.
$AH=AD. sin60^o=\frac{\sqrt{3}}{2}.a$
$=> AI= \frac{SA.AH}{SH}=\frac{a.\frac{\sqrt{3}}{2}.a}{a.\sqrt{1^2+(\frac{\sqrt{3}}{2})^2}}=\frac{\sqrt{21}}{7}.a$.
Câu b chắc có cách ngắn hơn ạ :v, căn bản là bí quá nên em dùng cả thế tích hình chóp nữa....
b) Gọi giao điểm của $(\alpha)$ với $AB, SB, SC, DC$ lần lượt là $M, N, P, Q$.
Thể tích khối chóp: $V=\frac{1}{3}.S.h$( h là chiều cao, S là diện tích mặt đáy).
ABCD là hình thang.
$S_{ABCD}=\frac{1}{2}.(a+2a).\frac{\sqrt{3}}{2}a=\frac{3\sqrt{3}.a^2}{4}$.
$V_{S.ABCD}=\frac{1}{3}.SA.S_{ABCD}=\frac{1}{3}.a.\frac{3\sqrt{3}.a^2}{4}=\frac{a^3\sqrt{3}}{4}$.
Lại có: $V_{S.ABCD}=\frac{1}{3}.d(B,(SAD)).S_{SAD}$
$=> d(B,(SAD))=\frac{V_{S.ABCD}}{\frac{1}{3}.S_{SAD}}=\frac{\frac{a^3\sqrt{3}}{4}}{\frac{1}{3}.\frac{1}{2}.a.a}=\frac{a.3\sqrt{3}}{2}$.
Do $(MNPQ)//(SAD)=>d(M,(SAD))=d((MNPQ),(SAD))=\frac{a\sqrt{3}}{4}$
Lại có: $\frac{d(M,(SAD))}{d(B,(SAD))}=\frac{MA}{BA}=> MA=\frac{\frac{a\sqrt{3}}{4}.2a}{\frac{a.3\sqrt{3}}{2}}=\frac{a}{3}$.
Theo định lí Ta-let: $\frac{MB}{AB}=\frac{MN}{SA}=>MN=\frac{(2a-\frac{a}{3}).a}{2a}=\frac{5a}{6}$
$MN//SA$ nên $MN \perp (ABCD)=> MN \perp MQ$
$AMQD$ là hình bình hành nên $MQ=AD=a$.
$S_{MNQ}=\frac{1}{2}.NM.MQ=\frac{1}{2}.\frac{5a}{6}.a=\frac{5a^2}{12}$
(Cái thiết diện này hình như chả phải hình gì nên em chia làm 2 phần để tính diện tích vậy @@)
$SD=\sqrt{a^2+a^2}=\sqrt{2}a$.
Theo Ta-let:$ \frac{PQ}{SD}=\frac{QC}{CD}=>PQ=\frac{\sqrt{2}.a.(a-\frac{a}{3})}{a}=\frac{a.2\sqrt{2}}{3}$
$\Delta NMQ$ vuông tại $M=>NQ=\sqrt{NM^2+MQ^2}=\sqrt{(\frac{5}{6}.a)^2+a^2}=\frac{\sqrt{61}}{6}a$
Gọi $d$ là đường thằng đi qua $S$ song song với $AB$ và $CD$
$=> d=(SAB) \cap (SCD)$.
Theo định lí về giao tuyến của 3 mặt phẳng $=> MN \cap PQ=K(K \in d)$.
Ta c/m được: $\Delta SAD= \Delta KMQ$=> $\widehat{ASD}=\widehat{MKQ}=45^o$.
$NK=MK-MN=a-\frac{5a}{6}=\frac{a}{6}$
$KP=KQ-PQ=\sqrt{2}.a-\frac{a.2\sqrt{2}}{3}=\frac{\sqrt{2}}{3}a$
Sử dụng định lí cos cho $\Delta KNP$: $NP=\sqrt{KN^2+KP^2-2.KN.KP.cos45}=\sqrt{(\frac{a}{6})^2+(\frac{\sqrt{2}}{3}a)^2-2.\frac{\sqrt{2}}{3}a.\frac{a}{6}.\frac{\sqrt{2}}{2}}=\frac{\sqrt{5}.a}{6}$.
Dùng công thức Hê rông tính $S_{NQP}$.
$S_{NPQ}=...$
Cái này ra số lẻ lắm @@.
Kết quả chưa ra nhưng mà em tiếc công gõ nên vẫn gửi bài ạ, có khi đúng là sai đề rùi :<<
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
