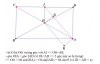
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm O, AB=2AD=2a, SA vuông góc với mặt phẳng (ABCD), SA=a. Gọi I là trung điểm của cạnh CD. Tính khoảng cách giữa đường thẳng SO và đường thẳng AI theo a?
Bài này bạn có thể làm như sau:
Qua O kẻ đường thẳng d song song với AI, từ A kẻ AK vuông góc với đường thẳng d và cắt đường thẳng d tại K. Ta có: AI // OK => AI // (SOK) => khoảng cách giữa đường thẳng AI và SO chính bằng khoảng cách từ A tới mặt phẳng (SOK).
Từ A kẻ AH vuông góc với SK, ta có: OK vuông góc với SA và AK => OK vuông góc với mặt phẳng (SAK) => OK vuông góc với AH mà AH cũng vuông góc với SK => AH vuông góc với mặt phẳng SAK hay AH chính là khoảng cách từ A tới mặt phẳng (SAK). Áp dụng công thức tính độ dài đường cao trong tam giác vuông SAK ta sẽ tính được độ dài AH: 1/AH^2 = 1/SA^2 + 1/AK^2
để tính độ dài AK ta có: AK = OI.sin(OIA) = OI.sin(IAD) = OI.sin45
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
