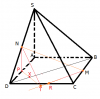
Mình xin phép trao đổi về một cách làm QUYỀN LỰC nhất có các bài toán có chân đường vuông góc:
Bước 1: Giá nào bạn cũng phải quy về mặt phẳng đáy đối với hình chóp để công việc diễn ra đơn giản nhất: Đối với bài này, dễ thấy BD thuộc mặt đáy nên cơ bản là phải quy về mặt phẳng (ABCD).
Bước 2: Kẻ đường thẳng qua M (vì M thuộc ABCD nên qua M cho đơn giản) đường thẳng song song với BD (ở đây là MR); xác định chân đường vuông góc của N xuống AD luôn là P ( tức kẻ NP // SA), PR cắt BD lại X.
Bước 3: tính d(P, (MNR)), để tính được khoảng cách này buộc phải tính NP và d(P, MR) mà d (P,MR) = d(P, DP) + d ( X, MR); khoảng cách từ PX chính là đoạn PX (với PX vuông góc BP) cái này bạn áp dụng nhanh talex để giải sẽ ổn, còn d(X,MR) thực chất do MR//BD nên d(X,BD) = d(M, PD) và dù gì M và P cũng đối xứng qua TÂM của ABCD nên d(P,BD) = d(M, BD) = d(X, BD), như vậy, gọi khoảng cách d(P,(MNR)) = h ta có 1/h^2 = 1/NP^2 + 1/d(P, MR)^2
Bước 4 sau khi có được d(P,(MNR)) dùng định lý talex: d(P,(MNR)) / 2 = d(X;MRN), từ đó suy ra d(DB;(MNR)) rồi suy ra được d(DB, MN)
Có khi là cách này sẽ khó và đòi hỏi bạn phải rõ việc mình làm nhưng mình cảm thấy đây là cách quyền lực trong khi đang thiếu ý tưởng. Chúc bạn thành công. Nếu mình có gì sơ sót bạn nhắc nhở nhé, cảm ơn bạn
View attachment 54304
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.