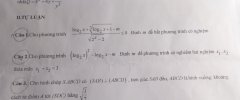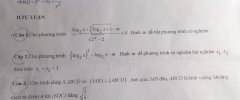1. Bất phương trình tương đương với [imath]x>1[/imath] và [imath]m \geq \log_2 x+\sqrt[3]{\log_2 x+1}[/imath]
Đặt [imath]t=\log _2 x[/imath] thì [imath]t >0[/imath]
Xét hàm số [imath]g(t)=t+\sqrt[3]{t+1}[/imath] trên [imath](0,+\infty)[/imath]
[imath]g'(t)=1+\dfrac{1}{3\sqrt[3]{(t+1)^2}>0[/imath]
Ta có bảng biến thiên như sau:
[math]\begin{array}{c|ccc} x & 0 & & +\infty \\ \hline y' & & + \\ \hline & & & +\infty \\ & & \nearrow & \\ y & 1 & & \end{array}[/math]Từ đó để bất phương trình [imath]g(x) \leq m[/imath] có nghiệm thì [imath]m >1[/imath]
2. Đặt [imath]t=\log_2 x[/imath] thì phương trình trở thành [imath]t^2-t-m=0[/imath]. (1)
Ta thấy với mỗi nghiệm [imath]t[/imath] thì cho [imath]1[/imath] nghiệm [imath]x>0[/imath] nên để phương trình ban đầu có [imath]2[/imath] nghiệm thì (1) có 2 nghiệm.
[imath]\Leftrightarrow \Delta =1+4m>0 \Leftrightarrow m>-\dfrac{1}{4}[/imath]
Giả sử (1) có 2 nghiệm [imath]t_1,t_2[/imath] thì [imath]x_1=2^{t_1},x_2=2^{t_2}[/imath]
Áp dụng định lí Vi-ét ta có [imath]t_1+t_2=1,t_1t_2=-m[/imath]
Từ [imath]x_1+x_2=3 \Rightarrow 2^{t_1}+2^{1-t_1}=3[/imath]
Xét [imath]f(x)=2^x+2^{1-x}-3[/imath]
[imath]f'(x)=\ln 2 \cdot \dfrac{4^x-2}{2^x}=0 \Leftrightarrow x=\dfrac{1}{2}[/imath]
Vì [imath]f'(x)=0[/imath] có 1 nghiệm nên [imath]f(x)=0[/imath] có tối đa 2 nghiệm.
Mà [imath]f(0)=f(1)=0[/imath] nên [imath]f(x)=0[/imath] chỉ có [imath]2[/imath] nghiệm là [imath]x=0[/imath] và [imath]x=1[/imath].
Từ đó suy ra [imath]t_1=1[/imath] hoặc [imath]t_1=0[/imath]
[imath]\Rightarrow \left[\begin{array}{l} t_1=0,t_2=1\\t_1=1,t_2=0\end{array}\right.[/imath]
[imath]\Rightarrow m=0[/imath].
Nếu còn thắc mắc chỗ nào bạn hãy trả lời dưới topic này để được hỗ trợ nhé. Chúc bạn học tốt ^^
Ngoài ra, bạn tham khảo kiến thức tại topic này nha
[Ôn thi THPTQG] Tài Liệu Ôn Thi THPTQG Môn Toán Lớp 12 (1)
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
