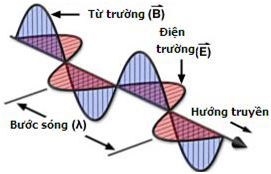
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chào các sĩ tử 2k4 

Vậy là một mùa thi đại học của các anh chị 2k3 đã đi qua rồi. Các bạn đã xem điểm chuẩn chưa nhỉ? Quá là kinh luôn đúng không

Thế nên, từ bây giờ, hãy tập trung ôn thi thật kĩ nhé, vừa đỡ tốn thời gian vừa thêm tự tin cho chính bản thân nè.

"Nhưng mà giờ ôn ở đâu???" Đây, ngay đây, chúng mình sẽ đi cùng các bạn đến hết kì thi thptqg năm 2022 để ôn thi Vật Lý nha. Đã quá đúng không Pepsi ơi

Không dong dài nữa, chào mừng các tân sĩ tử đến với:
I) Mục đích
IV) Nội quy
Còn chần chờ gì nữa mà không tham gia ôn tập cùng chúng mình nào. Hãy cùng nhau tạo nên những con số thật đẹp nhé.

Tham gia làm bài tập tại: [HOT] Ôn thi thptqg 2022 môn Vật Lý - phần bài tập
Góp ý cho chúng mình tại: [Góp ý] Ôn thi thptqg 2022 môn Vật Lý


Vậy là một mùa thi đại học của các anh chị 2k3 đã đi qua rồi. Các bạn đã xem điểm chuẩn chưa nhỉ? Quá là kinh luôn đúng không


Thế nên, từ bây giờ, hãy tập trung ôn thi thật kĩ nhé, vừa đỡ tốn thời gian vừa thêm tự tin cho chính bản thân nè.


"Nhưng mà giờ ôn ở đâu???" Đây, ngay đây, chúng mình sẽ đi cùng các bạn đến hết kì thi thptqg năm 2022 để ôn thi Vật Lý nha. Đã quá đúng không Pepsi ơi


Không dong dài nữa, chào mừng các tân sĩ tử đến với:
I) Mục đích
- Tạo cơ hội ôn tập, chuẩn bị cho kì thi thptqg năm 2022 cho các bạn tân sĩ tử 2k4
- Bổ sung kiến thức, cơ hội học vượt cho các bạn khoá sau
- Xây dựng thời khoá biểu học tập đúng đắn, khoa học
- Các bạn 2k4 cùng toàn thể thành viên Hocmai Forum
IV) Nội quy
- Hiện tại chúng mình có 2 topic: ôn lý thuyết và bài tập vận dụng.
- Ở đây là topic lý thuyết, tất cả thành viên không được trao đổi ở đây.
- Không được trao đổi môn học khác.
- Quyết định của BQT là cao nhất.
- Mọi vi phạm sẽ được xử lý theo nội quy của Hocmai Forum.
Còn chần chờ gì nữa mà không tham gia ôn tập cùng chúng mình nào. Hãy cùng nhau tạo nên những con số thật đẹp nhé.


Tham gia làm bài tập tại: [HOT] Ôn thi thptqg 2022 môn Vật Lý - phần bài tập
Góp ý cho chúng mình tại: [Góp ý] Ôn thi thptqg 2022 môn Vật Lý












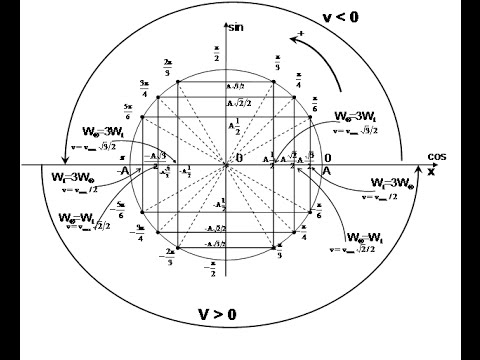
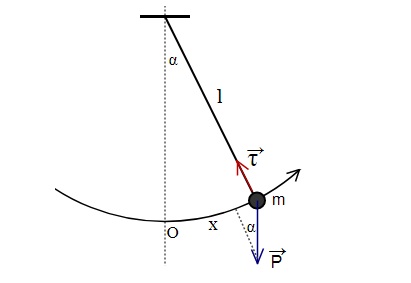


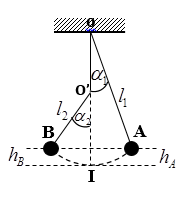


.png)