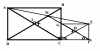
Cho hình chữ nhật ABCD có I là giao điểm của 2 đường chéo AC và BD. Lấy M bất kì thuộc IB . Vẽ điểm E đối xứng với A qua M.Gọi H là trung điểm của CE.Tứ giác IMEC là hình thang, tứ giác IMHC là hình bình hành. Đường thẳng MH cắt BC tại G và cắt DC tại F và tam giác HCF cân, hãy chứng minh GCFE là hình chữ nhật
ta có: HC=HE(gt)
mà t,g CHG cân nên HC = HF => HF=HC=HE=1/2CE=> tam giác CEF có HF là trung tuyến và HF = 1/2 CE => t,g CEFvuông tại F (1)
góc F = 90
[tex]\widehat{GCH}=\widehat{GCF}-\widehat{HCF}.....
....\widehat{EFH}= \widehat{EFC}-\widehat{HFC}
....\widehat{HCF}=\widehat{HFC}(gt) \rightarrow .....\widehat{GCH}=\widehat{EFH}
.....\Delta GHC và \Delta EHF có \widehat{GCH}=\widehat{EFH}
..... \widehat{GHC}=\widehat{EHF}(đối đỉnh)
.....CH=FH(gt) \rightarrow
..... \Delta GHC = \Delta EHF(g-c-g)
....\rightarrow GH=HF
...\rightarrow H trung điểm của GF
.....mà theo đề H là trung điểm của GE
...... \rightarrow GEFC là hình bình hành và có \widehat{EFC}=90^{\circ}
........ \rightarrow GEFC là HCN[/tex]
khi gõ công thức s nó ko xuống dòng nên nếu ko hiểu thì hỏi lại nhé
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
