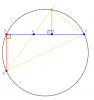
Thường thường lớp 9 mới học tới đường tròn, nên xin phép bạn cho mình sử dụng kiến thức lớp 9.
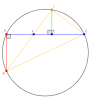
Gọi tên các điểm $A, B, D, E$ như hình. Gọi thêm $F$ là giao điểm của $AE$ và $BD$, $C$ là giao điểm của $AE$ và đường tròn.
Ta có $\widehat{BDC} = \widehat{BAC} = 90^\circ$ (góc nội tiếp chắn cung $BC$)
Áp dụng định lý Ta-lét: $$\dfrac{FE}{FA} = \dfrac{ED}{AB} = \dfrac{8}{12} = \dfrac{2}{3}$$
$\implies \dfrac{FE}{EA} = \dfrac{2}{5}$ ($FE$ chiếm $2$ phần, $FA$ chiếm $3$ phần thì $EA$ chiếm $5$ phần)
$\implies FE = \dfrac{2}{5} \cdot EA = \dfrac{2}{5} \cdot 15 = 6$
Xét $\triangle{FDC}$ vuông tại $D$, có $DE^2 = FE \cdot EC$ (hệ thức lượng)
$\implies EC = \dfrac{DE^2}{FE} = \dfrac{8^2}{6} = \dfrac{32}3$
$\implies AC = AE + EC = 15 + \dfrac{32}3 = \dfrac{77}3$
Xét $\triangle{ABC}$, có $BC^2 = AB^2 + AC^2$ (định lý Pytago)
$\implies BC^2 = 12^2 + \left(\dfrac{77}3\right)^2 = \dfrac{7225}9$
$\implies BC = \dfrac{85}3$
Do $BC$ là đường kính của đường tròn (do $\widehat{BAC} = 90^\circ$) nên bán kính đường tròn là $\dfrac{BC}2 = \dfrac{85}6$
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
