[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Cho góc xOy=90 độ
Trên tia Ox lấy điểm A sao cho OA=2cm
Trên tia Oy lấy điểm N bất kỳ
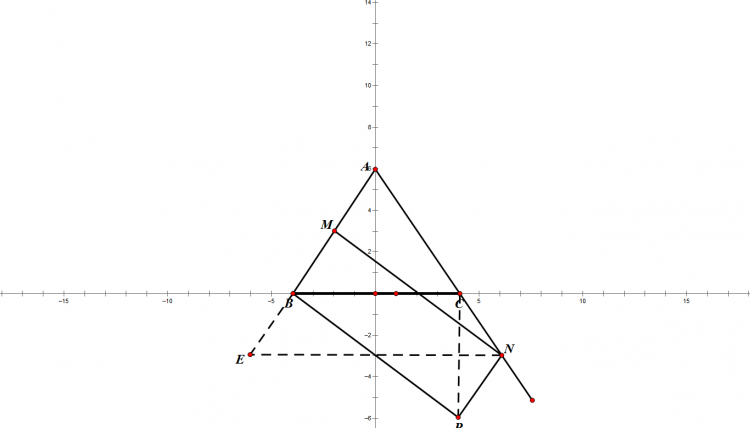
Dựng tam giác MAN vuông cân tại A.
Tìm quỹ tích điểm M.
-Mọi người cho em hỏi quỹ tích là gì? Em năm nay học lớp 9 và k hề biết quỹ tích
-Mọi người giúp em với, gấp lắm ạ!!
Trên tia Ox lấy điểm A sao cho OA=2cm
Trên tia Oy lấy điểm N bất kỳ
Dựng tam giác MAN vuông cân tại A.
Tìm quỹ tích điểm M.
-Mọi người cho em hỏi quỹ tích là gì? Em năm nay học lớp 9 và k hề biết quỹ tích
-Mọi người giúp em với, gấp lắm ạ!!