- 24 Tháng mười 2018
- 1,616
- 1,346
- 216
- 25
- TP Hồ Chí Minh
- Đại học Sư phạm Kỹ thuật TP Hồ Chí Minh
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
xét hình nón cụt (H) có:
- bán kính đáy nhỏ là [tex]r_1[/tex]
- bán kính đáy lớn là [tex]r_2[/tex]
- chiều cao là h.
- đường sinh là l.
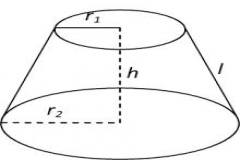
- [tex]l=\sqrt{h^2+(r_2-r_1)^2}[/tex]
- diện tích xung quanh hình nón cụt: [tex]S_{xq}=\pi.(r_1+r_2).l[/tex]
- diện tích toàn phần nón cụt: [tex]S_{tp}=S_{xq}+S_{2d}=\pi.(r_1+r_2).l+\pi.r_1^2+\pi.r_2^2[/tex]
- thể tích khối nón cụt: [tex]V=\frac{\pi.h}{3}(r_1^2+r_1.r_2+r_2^2)[/tex]
ví dụ 1: một ly nước có dạng hình nón có thể tích phần chứa nước là 100 [tex]cm^3[/tex], người ta đổ nước vào ly sao cho mực nước bằng 1/2 ly. tính thể tích lượng nước có trong ly.
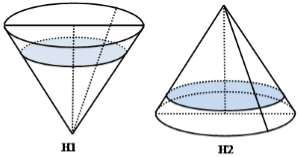
giải:
theo định lý talet, chiều cao của nược trong ly là 1/2h, nên bán kính của mặt nước cũng là 1/2R.
thể tích của ly tính theo bán kính đáy và chiều cao:
[tex]V=\frac{1}{3}\pi.R^2.h[/tex]
thể tích của nước tính theo bán kính đáy và chiều cao:
[tex]V'=\frac{1}{3}.\pi.(\frac{R}{2})^2.\frac{h}{2}=\frac{V}{8}[/tex]
vậy nên thể tích của nước trong ly là:
[tex]V'=\frac{100}{8}=\frac{25}{2}cm^3[/tex]
ví dụ 2: một ly có phần trên đựng nước là khối có dạng hình nón với chiều cao là h. người ta đổ nước vào ly sao cho mực nước cao bằng 1/3 ly. khi lật ngược ly lại, chiều cao của mực nước trong ly là bao nhiêu.
giải:
theo định lý talet, chiều cao của nược trong ly là 1/3h, nên bán kính của mặt nước cũng là 1/3R.
thể tích của ly tính theo bán kính đáy và chiều cao:
[tex]V=\frac{1}{3}\pi.R^2.h[/tex]
thể tích của nước tính theo bán kính đáy và chiều cao:
[tex]V'=\frac{1}{3}.\pi.(\frac{R}{3})^2.\frac{h}{3}=\frac{V}{27}[/tex]
thể tích này bằng thể tích nước khi lật ngược ly lại.
gọi h' là mực nước cần tìm, theo đinh lý pytago ta tìm được:
[tex]R'=\frac{R}{h}(h-h')[/tex]
thê tích khi đó:
[tex]V''=\frac{1}{3}.\pi.h'.(R^2+R.R'+R'^2)=\frac{\pi.R^2.h'}{3h^2}.(h'^2-3h.h'+3h^2)=\frac{\pi.R^2.h}{81}[/tex]
[tex]27h'.(h'^2-3h.h'+3h^2)-h^3=0[/tex]
chia cả tử và cho h, ta được 1 phương trình bậc 3 theo t, với [tex]t=\frac{h'}{h}[/tex].
giải phương trình trên ta tìm được mực nước.
- bán kính đáy nhỏ là [tex]r_1[/tex]
- bán kính đáy lớn là [tex]r_2[/tex]
- chiều cao là h.
- đường sinh là l.
- [tex]l=\sqrt{h^2+(r_2-r_1)^2}[/tex]
- diện tích xung quanh hình nón cụt: [tex]S_{xq}=\pi.(r_1+r_2).l[/tex]
- diện tích toàn phần nón cụt: [tex]S_{tp}=S_{xq}+S_{2d}=\pi.(r_1+r_2).l+\pi.r_1^2+\pi.r_2^2[/tex]
- thể tích khối nón cụt: [tex]V=\frac{\pi.h}{3}(r_1^2+r_1.r_2+r_2^2)[/tex]
ví dụ 1: một ly nước có dạng hình nón có thể tích phần chứa nước là 100 [tex]cm^3[/tex], người ta đổ nước vào ly sao cho mực nước bằng 1/2 ly. tính thể tích lượng nước có trong ly.
giải:
theo định lý talet, chiều cao của nược trong ly là 1/2h, nên bán kính của mặt nước cũng là 1/2R.
thể tích của ly tính theo bán kính đáy và chiều cao:
[tex]V=\frac{1}{3}\pi.R^2.h[/tex]
thể tích của nước tính theo bán kính đáy và chiều cao:
[tex]V'=\frac{1}{3}.\pi.(\frac{R}{2})^2.\frac{h}{2}=\frac{V}{8}[/tex]
vậy nên thể tích của nước trong ly là:
[tex]V'=\frac{100}{8}=\frac{25}{2}cm^3[/tex]
ví dụ 2: một ly có phần trên đựng nước là khối có dạng hình nón với chiều cao là h. người ta đổ nước vào ly sao cho mực nước cao bằng 1/3 ly. khi lật ngược ly lại, chiều cao của mực nước trong ly là bao nhiêu.
giải:
theo định lý talet, chiều cao của nược trong ly là 1/3h, nên bán kính của mặt nước cũng là 1/3R.
thể tích của ly tính theo bán kính đáy và chiều cao:
[tex]V=\frac{1}{3}\pi.R^2.h[/tex]
thể tích của nước tính theo bán kính đáy và chiều cao:
[tex]V'=\frac{1}{3}.\pi.(\frac{R}{3})^2.\frac{h}{3}=\frac{V}{27}[/tex]
thể tích này bằng thể tích nước khi lật ngược ly lại.
gọi h' là mực nước cần tìm, theo đinh lý pytago ta tìm được:
[tex]R'=\frac{R}{h}(h-h')[/tex]
thê tích khi đó:
[tex]V''=\frac{1}{3}.\pi.h'.(R^2+R.R'+R'^2)=\frac{\pi.R^2.h'}{3h^2}.(h'^2-3h.h'+3h^2)=\frac{\pi.R^2.h}{81}[/tex]
[tex]27h'.(h'^2-3h.h'+3h^2)-h^3=0[/tex]
chia cả tử và cho h, ta được 1 phương trình bậc 3 theo t, với [tex]t=\frac{h'}{h}[/tex].
giải phương trình trên ta tìm được mực nước.
