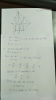Toán 11 Hình không gian

[Như Thủy.]

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

1.Cho hình chóp SABCD có đáy ABCD là hbh tâm O.Gọi M,N lần lượt là td của SD,SB,P là trung điểm của OC.
a.Tìm giao tuyến của 2 mp (MNP) vs (ABCD)
b.Tìm giao điểm K của SA và (MNP).Cm: PK // (SCD)
c.Mặt phẳng ([tex]\alpha[/tex]) qua N // SO và AD.([tex]\alpha[/tex]) cắt AB,CD,SC lần lượt tại E,F,T.Tứ giác NEFT là hình gì? Cm.
2.Cho hình chóp SABCD có đáy ABCD là hthang với đáy lớn AD,AD=2BC,AC giao BD tại O.Gọi M là trung điểm SD.
a.Tìm giao tuyến của (SAD) vs (MBC)
b.Tìm giao điểm của OM và (SAB)
c.Gọi G là trọng tâm tam giác SBC.Cm : OG//(SAD)
d.(Vẽ hình riêng) Gọi H là trọng tâm tam giác SAB,mp (P) qua H,// AD và SO.(P) cắt AB,CD,SA,SD, lần lượt tại E,F,T,Q.Tứ giác EFQT là hình gì.Cm

 

[hoccungban01]

 

[hoccungban01]

 

[iceghost]

2.Cho hình chóp SABCD có đáy ABCD là hthang với đáy lớn AD,AD=2BC,AC giao BD tại O.Gọi M là trung điểm SD.
a.Tìm giao tuyến của (SAD) vs (MBC)
b.Tìm giao điểm của OM và (SAB)
c.Gọi G là trọng tâm tam giác SBC.Cm : OG//(SAD)
d.(Vẽ hình riêng) Gọi H là trọng tâm tam giác SAB,mp (P) qua H,// AD và SO.(P) cắt AB,CD,SA,SD, lần lượt tại E,F,T,Q.Tứ giác EFQT là hình gì.Cm

a) Ta có $M \in SD \subset (SAD)$ và $M \in (MBC) \implies M \in (SAD) \cap (MBC)$
Mà $AD \parallel BC$, $AD \in (SAD)$ và $BC \in (MBC)$
Khi đó gọi $d$ qua $M$ và $d \parallel AD \parallel BC$ thì $d = (SAD) \cap (MBC)$
b) Do $\dfrac{OB}{OD} = \dfrac{BC}{AD} = \dfrac12 \ne 1 = \dfrac{MC}{MD}$ nên gọi $J$ là giao điểm của $OM$ với $SB$. Khi đó $J \in OM$ và $J \in SB \subset (SAB)$ nên $J = OM \cap (SAB)$
c) Gọi $P= SG \cap BC$ và $Q = PO \cap AD$, ta có $\dfrac{PG}{GS} = \dfrac12 = \dfrac{PO}{OQ}$ nên $OG \parallel SQ$. Do $SQ \subset (SAD)$ nên $OG \parallel (SAD)$

 

[hoccungban01]