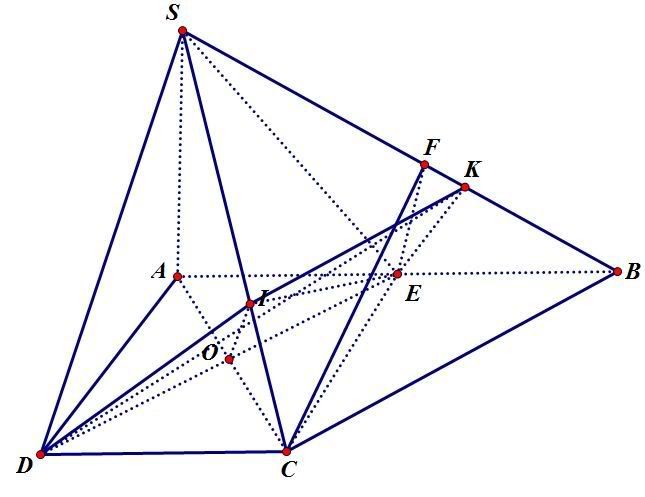
cho hinh chop S.ABCD va SA vuong voi mat phang day .ABCD la hinh thang vuog tai A,D .co AB=2a, AD=DC=a.tinh goc giua : a,mp(SBC)va(ABC) b,mp(SAB)va(SBC) c,mp(SBC)va(SCD)
a) mp(SBC)va(ABC)
Gọi E là trung điểm AB
Trong tam giác ABC: AC=BC=CE => tam giác ABC vuông tại C
mặt khác: SA vuông góc CB
=> CB vuông góc (SAC)
Mặt phẳng (SAB) và (SBC) cắt nhau theo giao tuyến BC vuoong góc (SAC)
(SAC) cắt (SAB) theo giao tuyến SA
(SAC) cắt (SBC) theo giao tuyến SC
=> Góc tạo bởi hai mặt phẳng (SAB) và (SBC) là góc SCA
Tam giác SAC vuông tại A
tanSCA = SA/AC
Vậy góc tạo bởi hai mặt phẳng (SAB) và (SBC) là arctan (SA/AC)
b,mp(SAB)va(SBC)
Hai mặt phẳng (SAB) và (SBC) cắt nhay theo giao tuyến SB
Kẻ EF vuông góc SB
Ta có:
CE vuông góc AB và CE vuông góc SA => CE vuông góc (SAB)
=> CE vuông góc SB
Vậy SB vuông góc (CEF)
(CEF) cắt (SAB) theo giao tuyến EF
(CEF) cắt (SBC) theo giao tuyến CF
=> Góc tạo bởi hai mặt phẳng (SAB) và (SBC) là CFE
Tam giác CFE vuông tại E
tanCFE= CE/EF
mặt khác, tam giác BFE và tam giác BAS đồng dạng ( tam giác vuông có chung góc B)
=> FE/AS = BE/BS => FE = BE*AS/BS
Vậy góc tạo bởi hai mặt phẳng (SBA) và (SBC) là arctan CE/EF
c,mp(SBC)va(SCD
Gọi O là giao điểm của DE và AC
ta có: AECD là hình vuông => AC vuông góc DE
mặt khác DE vuông góc SA
=> DE vuông góc (SAC) => DE vuông góc SC
Kẻ OI vuông góc SC tại I
=> (DIE) vuông góc SC
Hai mặt phẳng (SCB) và (SCD) cắt nhau theo giao tuyến SC
(DIE) cắt (SCD) theo giao tuyến DI
Ta có: BC//DE, BC không thuộc (DIE), DE thuộc (DIE) => BC// (DIE)
(DIE) cắt (SBC) theo giao tuyến qua I và song song BC là IK ( K thuộc SB)
Góc giữa mặt phẳng (SBC) và (SCD) là góc DIK
Tam giác CIO đồng dạng tam giác CAS ( hai tác giác vuông có góc C chung)
=> IO/AS = CO/CS => IO = CO*AS/CS = CO*AS / (căn bậc 2 (CA^2+AS^2))
DI = căn bậc 2 ( DO^2 + OI^2)
Ta có: IK//CB
=> IK/CB =SI/SC
=> IK = SI * CB/SC
mặt khác, trong tam giác vuông CIO:
CI = căn bậc 2 (OC^2-OI^2)
=> IC/SC =... => SI/SC
OIKE là hình bình hành nên OI=EK
Trong tam giác vuông DEK ( vuông tại E)
DK =căn bậc 2 ( DE^2+EK^2)
ta có: CosDIK= (ID^2+IK^2-DK^2 )/(2DI*DK)
=> Góc tạo bởi 2 mặt phẳng (SCD) và (SCB) là arcos DIK
(Vì bạn ko cho biết SA nên mình chỉ hướng tính thôi, bạn tự thay số nha)
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
