Toán 9 Hình học

[Lucyna]

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

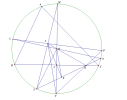
Cho [imath]\Delta ABC[/imath] nội tiếp [imath](O)[/imath] , ngoại tiếp [imath](I)[/imath] . [imath]M[/imath] là điểm chính giữa cung [imath]BAC[/imath] . [imath]J[/imath] là trung điểm [imath]BC[/imath] . [imath]MI[/imath] cắt [imath](O)[/imath] tại [imath]T[/imath] khác [imath]M[/imath] . [imath]OI[/imath] cắt [imath]BC[/imath] tại [imath]K[/imath] ,
[imath]KT[/imath] cắt [imath]IJ[/imath] tại [imath]X[/imath] . Chứng minh [imath]X,O,I,T[/imath] đồng viên

Mọi người giúp em câu này với ạ!!

 

[kido2006]

Gọi Y là điểm chính giữa cung BC không chứa A
Gọi [imath]TK∩(O)[/imath] tại N khác T , [imath]NO ∩(O)[/imath] tại L, [imath]LI∩(O)=P[/imath]
Gọi [imath]PY ∩ NT[/imath] tại K'
Áp dụng định lí Pascal cho [imath]\dbinom{MPN}{LTY}[/imath]
[imath]\Rightarrow \overline{I,O,K} \Rightarrow K≡K'[/imath]

Dễ chứng minh [imath]YB^2=YI^2=YJ.YM=YK.YP[/imath]
[imath]\Rightarrow \widehat{OIX}=\widehat{KIY}-\widehat{JIY}=\widehat{P}-\widehat{M}=\dfrac{1}{2}sd \overset{\cap }{TL}=\widehat{LNT}=\widehat{OTX}[/imath]
=> dpcm


Nếu còn thắc mắc chỗ nào bạn hãy trả lời dưới topic này để được hỗ trợ nhé ^^
Chúc bạn học tốt ^^
Ngoài ra, bạn tham khảo kiến thức tại đây nhé
[Chuyên đề HSGQG] Định lý LTE, cấp của số nguyên và phương trình nghiệm nguyên chứa lũy thừa