Toán 9 Hình học

[_Error404_]

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

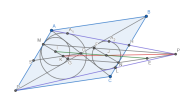
Cho hình bình hành [imath]ABCD[/imath] có đường chéo [imath]AC[/imath] cắt [imath]BD[/imath] tại [imath]O[/imath]. Đường tròn [imath](I)[/imath] nội tiếp [imath]\Delta OAD[/imath] tiếp xúc [imath]AD[/imath] tại [imath]M[/imath]. Đường tròn [imath](J)[/imath] nội tiếp [imath]\Delta OBC[/imath] tiếp xúc [imath]BC[/imath] tại [imath]N[/imath].
a) Chứng minh [imath]M,N[/imath] đối xứng qua [imath]O[/imath].
b) Lấy [imath]P[/imath] khác [imath]O[/imath] sao cho [imath]PA,PD[/imath] tiếp xúc [imath](J)[/imath]. Chứng minh [imath]PA-PD=NC-NB[/imath]
c) Gọi [imath]S[/imath] là trung điểm [imath]AD[/imath]. Chứng minh [imath]OS[/imath] đi qua tâm đường tròn nội tiếp [imath]\Delta PAD[/imath].
Mọi người giúp e câu c với (Trích đề thi thử vòng 1 chuyên KHTN lần 2)

 

[7 1 2 5]

Từ câu 2) ta có [imath]PA-PD=NC-NB=MA-MD[/imath]. Điều này sẽ suy ra [imath]M[/imath] là tiếp điểm của đường tròn nội tiếp [imath]\Delta PAD[/imath].
Gọi [imath]K[/imath] là tâm đường tròn nội tiếp [imath]\Delta PAD[/imath] thì [imath]KM \perp AD \Rightarrow K,I,M[/imath] thẳng hàng.
Mặt khác, ta thấy [imath]PK, PJ[/imath] là phân giác của [imath]\Delta PAD[/imath] nên [imath]P,K,J[/imath] thẳng hàng.
Giả sử [imath]PA[/imath] tiếp xúc [imath](I),(J)[/imath] tại [imath]A_1,A_2[/imath]. [imath]MI[/imath] cắt [imath](I)[/imath] tại điểm thứ hai là [imath]G[/imath], đường thẳng qua [imath]J[/imath] song song với [imath]IM[/imath] cắt [imath]PA[/imath] tại [imath]F[/imath].
Khi đó theo định lý Thales ta có [imath]\dfrac{PJ}{PK}=\dfrac{JA_2}{KA_1}=\dfrac{JF}{KM}[/imath]
Mà [imath]KM=KA_1 \Rightarrow JA_2=JF[/imath] hay [imath]F \in (J)[/imath]
Lại có: Bán kính của [imath](I)[/imath] và [imath](J)[/imath] bằng nhau (do 2 đường tròn đối xứng qua [imath](O)[/imath]) nên [imath]JF=IM[/imath]
[imath]\Rightarrow \dfrac{PJ}{PK}=\dfrac{MI}{MK} \Rightarrow IJ \parallel MP[/imath]
Ta thấy [imath]MG \parallel FN[/imath](cùng vuông góc [imath]AD[/imath] và [imath]BC[/imath]), [imath]I,J[/imath] là trung điểm [imath]MG,FN[/imath] và [imath]IJ \parallel MF[/imath] nên ta chứng minh được [imath]GN \parallel IJ \parallel MP[/imath]
Giả sử [imath]IJ[/imath] cắt [imath]NP[/imath] tại [imath]E[/imath] thì theo định lý Thales ta có [imath]EN=EP[/imath]
Tới đây em chỉ cần chứng minh [imath]PN \parallel DC[/imath] là được nhé. Em có thể chứng minh bằng cách chứng minh [imath](K)[/imath] với [imath](J)[/imath] có tiếp tuyến chung song song với [imath]AD[/imath].

Nếu còn thắc mắc chỗ nào bạn hãy trả lời dưới topic này để được hỗ trợ nhé. Chúc bạn học tốt ^^
Ngoài ra, bạn tham khảo kiến thức tại topic này nha
Ôn tập toán các dạng bài hình học 9