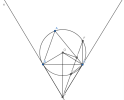
a) Do [imath]BD[/imath] và [imath]CD[/imath] lần lượt là 2 tiếp tuyến tại [imath]B[/imath] và [imath]C[/imath] nên ta có [imath]\widehat{DBO}=90^o[/imath] và [imath]\widehat{DCO}=90^o[/imath]
[imath]\Rightarrow \widehat{DBO}+\widehat{DCO}=180^o[/imath] nên tứ giác [imath]BDCO[/imath] nội tiếp
b) Xét [imath]\Delta DCE[/imath] và [imath]\Delta DFC[/imath] có
[imath]\begin{cases}\widehat{CDF} chung \\ \widehat{DCE}=\widehat{DFC} (=\dfrac{1}{2}\stackrel\frown{EC}) \end{cases}[/imath]
[imath]\Rightarrow \Delta DCE[/imath] đồng dạng [imath]\Delta DFC[/imath] (g-g)
[imath]\Rightarrow \dfrac{DC}{DF}=\dfrac{DE}{DC}[/imath]
[imath]\Rightarrow DC^2=DE.DF[/imath]
c) Do [imath]AB \parallel DF[/imath] nên [imath]\widehat{ABx}=\widehat{BDF}[/imath]
Lại có [imath]\widehat{ABx}=\widehat{ACB} (=\dfrac{1}{2}\stackrel\frown{AB})[/imath]
Nên [imath]\widehat{BDF}=\widehat{ACB}[/imath]
[imath]\Leftrightarrow \widehat{BDO}+\widehat{ODF}=\widehat{OCB}+\widehat{OCA}[/imath]
Mà [imath]\widehat{OCB}=\widehat{BDO}[/imath] (do tứ giác [imath]BDCO[/imath] nội tiếp) nên [imath]\widehat{ODI}=\widehat{OCI}[/imath]
[imath]\Rightarrow[/imath] tứ giác [imath]ODCI[/imath] nội tiếp.
d) Do tứ giác [imath]ODCI[/imath] nội tiếp nên [imath]\widehat{OID}=\widehat{OCD}=90^o[/imath]
[imath]\Rightarrow OI \bot EF[/imath]
[imath]\Rightarrow I[/imath] là trung điểm [imath]EF[/imath]
e) Có [imath]\widehat{BAC}=60^o \Rightarrow \stackrel\frown{BC}=\widehat{BOC}=2\widehat{BAC}=120^o[/imath]
[imath]\Rightarrow[/imath] diện tích hình quạt [imath]OBC=\dfrac{1}{3}.S_{(O)}=\dfrac{16}{3}.\pi[/imath]
Gọi [imath]H[/imath] là giao điểm của [imath]OD[/imath] và [imath]BC[/imath] ta có [imath]OH \bot BC[/imath]
[imath]\Delta OBC[/imath] cân tại [imath]O[/imath] có [imath]\widehat{BOC}=120^o \Rightarrow \widehat{OBC}=30^o[/imath]
[imath]\Rightarrow OH =\dfrac{1}{2} OB =2 \Rightarrow BH=2\sqrt{3} \Rightarrow BC =2BH=4\sqrt{3} \Rightarrow S_{\Delta OBC}=4\sqrt{3}[/imath]
[imath]\Rightarrow[/imath] diện tích hình viên phấn tạo bởi dây [imath]BC[/imath] và [imath]\stackrel\frown{BC}=S_{OBC}-S_{\Delta OBC}[/imath]
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
