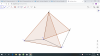
Phía nửa mặt phẳng bờ AB không chứa M lấy N sao cho AMN là tam giác đều
nên [tex]\widehat{CAB}=\widehat{MAN}[/tex]
[tex]\Leftrightarrow \widehat{CAM}+\widehat{MAB}=\widehat{MAB}+\widehat{BAN}[/tex]
[tex]\widehat{CAM}=\widehat{BAN}[/tex]
mà CA = BA và AM = AN
Vậy [tex]\Delta CAM=\Delta BAN[/tex]
Suy ra CM =BN
Ta có MA^2 = MB^2 + MC^2
nên MN^2 = MB^2 + BN^2
Nên tam giác MBN vuông tại B
Ta có [tex]\Delta CAM=\Delta BAN[/tex]
nên [tex]\widehat{ACM}=\widehat{ABN}[/tex]
[tex]\Leftrightarrow \widehat{MBN}=\widehat{ABM}+\widehat{ABN}=90^{\circ}[/tex]
[tex]\Leftrightarrow \widehat{ABM}+\widehat{ACM}=90^{\circ}[/tex]
[tex]\Leftrightarrow (60^{\circ}-\widehat{MBC})+(60^{\circ}-\widehat{MCB})=90^{\circ}[/tex]
[tex]\Leftrightarrow 120^{\circ}-(\widehat{MBC}+\widehat{MCB})=90^{\circ}[/tex]
[tex]\Leftrightarrow \widehat{MBC}+\widehat{MCB}=30^{\circ}[/tex]
[tex]\Rightarrow \widehat{BMC}=180^{\circ}-30^{\circ}=150^{\circ}[/tex]
Vậy [tex]\widehat{BMC}=150^{\circ}[/tex]
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
