Toán 9 hình học

[Lena1315]

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

Cho hình thoi ABCD có

 

[iceghost]

Mình giới thiệu cách dễ nhất, không hay lắm.

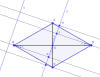
Qua $O$ kẻ $d'$ song song $d$ thì độ dài hình chiếu các cạnh trên $d$ cũng bằng hình chiếu trên $d'$.

Hạ các đoạn vuông góc $AH, BK, CI, DJ$.

Không mất tính tổng quát, giả sử đường thẳng $d$ sao cho $I, K, J, H$ thẳng hàng trên $d'$ theo thứ tự như trên hình.

đpcm $\iff A = HK^2 + IJ^2 + HJ^2 + IK^2 + 2AC^2$ không đổi
$A = (OH + OK)^2 + (OI + OJ)^2 + (OH - OJ)^2 + (OI - OK)^2 + 2AC^2$

Gọi cạnh hình thoi là $a$ và góc $\alpha$ tạo bởi $d'$ và $AC$ thì bạn tính tất cả các cạnh ở trên theo $a$ và $\alpha$, sau đó khai triển và rút gọn hết $\alpha$ là được.

Chú ý đẳng thức $\sin^2 \alpha + \cos^2 \alpha = 1$.