[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Cho tam giác $ABC$ và điểm $M$ bất kì nằm trên mặt phẳng chứa tam giác $ABC$. Đường thẳng $AM$ cắt $(B;BM)$, $(C;CM)$ lần lượt tại $P$ và $Q$. Vẽ đường kính $PD$ của $(B)$ và đường kính $QE$ của $(C)$. Chứng minh rằng ba điểm $D,M,E$ thẳng hàng.
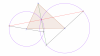
- LÊ NGỌC TÚ -