Cho tam giác ABC nội tiếp đường tròn (O). Tiếp tuyến tại B và C cắt nhau tại M. OM cắt MC tại I và AM cắt (O) tại N. Kẻ đường kính NP. Các đường thẳng PA và BC cắt nhau tại E. Gọi Q là giao điểm PC và BN. Chứng minh ME tiếp xúc với đường tròn ngoại tiếp tam giác OIQ. ( mọi người giúp em với ạ :< )
0844862486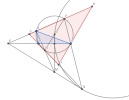
+ Chứng minh [imath]E,M,Q[/imath] thằng hàng
Gọi các giao điểm của [imath]3[/imath] đường thẳng [imath]BN,AP[/imath] và tiếp tuyến của [imath]C[/imath] với [imath](O)[/imath] là [imath]F,G,H[/imath] như hình vẽ.
Áp dụng định lý Menelaus cho [imath]\Delta FGH[/imath] có
[imath]Q,C,P[/imath] thẳng hàng ta được: [imath]\dfrac{QF}{QG}\cdot \dfrac{CG}{CH} \cdot \dfrac{PH}{PF}=1 \Rightarrow \dfrac{QF}{QG}=\dfrac{CH}{CG} \cdot \dfrac{PF}{PH}[/imath]
[imath]M,A,N[/imath] thẳng hàng ta được: [imath]\dfrac{MQ}{MH}\cdot \dfrac{AH}{AF} \cdot \dfrac{NF}{NG}=1 \Rightarrow \dfrac{MQ}{MH}=\dfrac{AF}{AH} \cdot \dfrac{NG}{NF}[/imath]
[imath]E,B,C[/imath] thằng hàng ta được: [imath]\dfrac{EH}{EF}\cdot \dfrac{BF}{BG} \cdot \dfrac{CG}{CH}=1 \Rightarrow \dfrac{EH}{EF}=\dfrac{BG}{BF} \cdot \dfrac{CH}{CG}[/imath]
Từ đó [imath]\dfrac{QF}{QG} \cdot \dfrac{MQ}{MH} \cdot \dfrac{EH}{EF} =\dfrac{CH^2}{CG^2} \cdot \dfrac{PF\cdot AF}{PH \cdot AH} \cdot \dfrac{BG \cdot NG}{BF \cdot NF}[/imath]
Mặt khác, ta lại có: [imath]PF \cdot AF = BF \cdot NF, PH \cdot AH=CH^2, BG \cdot NG=CG^2[/imath] nên [imath]\dfrac{QF}{QG} \cdot \dfrac{MQ}{MH} \cdot \dfrac{EH}{EF} =1[/imath]
Suy ra [imath]E,M,Q[/imath] thẳng hàng.
+ Chứng minh [imath]MQ[/imath] là tiếp tuyến.
Nhận thấy [imath]MI\cdot MO=MC^2[/imath] nên ta chỉ cần chứng minh [imath]MB=MC=MQ[/imath], hay [imath]Q[/imath] thuộc đường tròn [imath](M,MB)[/imath]
Ta có: [imath]\widehat{BQC}=\dfrac{1}{2}(\text{sđBP}-\text{sđNC})=\dfrac{1}{2}(\text{sđPN}-\text{sđBC})=\dfrac{1}{2}(180^o-\widehat{BOC})=\dfrac{1}{2}\widehat{BMC}[/imath]
[imath]\Rightarrow Q \in (M,MB)[/imath]
Từ đó ta có đpcm.
Nếu còn thắc mắc chỗ nào bạn hãy trả lời dưới topic này để được hỗ trợ nhé. Chúc bạn học tốt ^^
Ngoài ra, bạn tham khảo kiến thức tại topic này nha
Ôn tập toán các dạng bài hình học 9
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
