Toán 11 hình học không gian

[phuongluongthi434@gmail.com]

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

cho hình hộp ABCDA'B'C'D' có véc tơ AB=a véc tơ AD=b véc tơ AA'=c.gọi i là trung điểm B'C' k là giao điểm A'I VÀ B'D'. biễu diễn các véc tơ AI , AK , DK theo các véc tơ a,b,c

 

[quynhphamdq]

• Ta có :

[TEX]\overrightarrow{AC'} =\overrightarrow{ AB}+\overrightarrow{AD}+\overrightarrow{AA' }=\overrightarrow{a}+ \overrightarrow{b} +\overrightarrow{c}[/TEX]
[TEX]\overrightarrow{ AB'}=\overrightarrow{ AB} +\overrightarrow{ AA'} =\overrightarrow{a}+\overrightarrow{c} [/TEX]
Xét trong tam giá AB'C' , I là trung điểm B'C'
$\overrightarrow{ AI}=\frac{\overrightarrow{ AB'}+\overrightarrow{ AC'}}{2} = \frac{2\overrightarrow{a}+ \overrightarrow{b} +2\overrightarrow{c}}{2}$

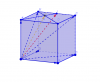
• Ta có : [TEX] \overrightarrow{ AK}=\overrightarrow{ AI} +\overrightarrow{IE}[/TEX]

Dễ dàng tính được[TEX] \overrightarrow{AC} =\overrightarrow{ A'C'}[/TEX] theo[TEX] \overrightarrow{ a}, \overrightarrow{ b}[/TEX]
[TEX]=> \overrightarrow{ A'I} => \overrightarrow{IE} => \overrightarrow{ AK}[/TEX]

• [TEX]\overrightarrow{ DK } =2/3 \overrightarrow{ B'D'} [/TEX]