G
girlhanoi_thickchoitroi_1995
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
1. Cho hình chóp S.ABCD có đáy là hình thang ABCD ( AB//CD) M là điểm di động trên cạnh SB
a, tim giao tuyến của mặt phẳng ( ADM ) và (SBC) ; (SBC) và (SAD) ; (SAC) và (SBD)
b , tìm giao điểm N của đường thẳng SC và (ADM)
c , gọi I là giao điểm của AN và DM chứng minh I nẳm trên 1 đường thẳng cố định
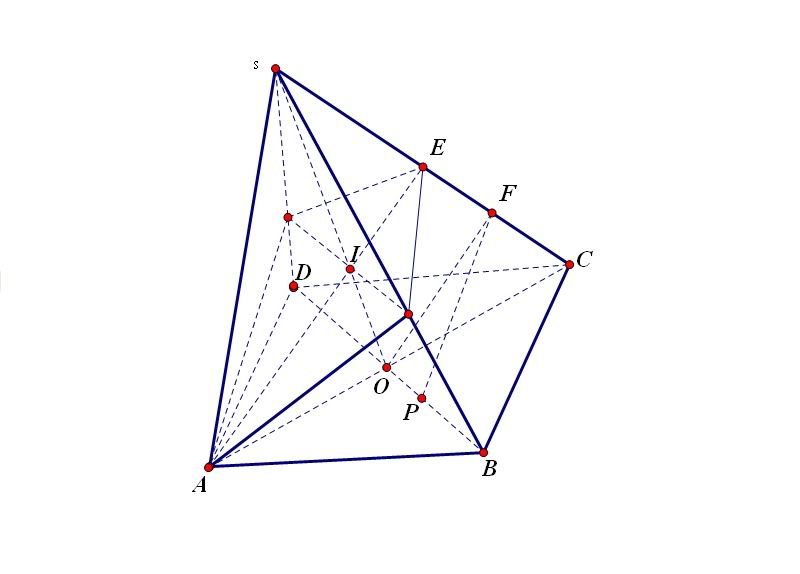
2. Cho hình chóp S.ABCD có đáy là hình vuông và tất cả các cạnh của hình chóp đều bằng a Gọi E là trung điểm của SC , F là trung điểm của EC Gọi ([tex]\alpha[/tex]) là mặt phẳng chứa AE và // với BD
a, xác định thiết diện của hình chóp cắt bới mặt phẳng ([tex]\alpha[/tex])
b, Gọi P là điểm bất kì thuộc cạnh BD . Chứng minh FP // với ([tex]\alpha[/tex])
c, tính diện tích ở câu a,
a, tim giao tuyến của mặt phẳng ( ADM ) và (SBC) ; (SBC) và (SAD) ; (SAC) và (SBD)
b , tìm giao điểm N của đường thẳng SC và (ADM)
c , gọi I là giao điểm của AN và DM chứng minh I nẳm trên 1 đường thẳng cố định
2. Cho hình chóp S.ABCD có đáy là hình vuông và tất cả các cạnh của hình chóp đều bằng a Gọi E là trung điểm của SC , F là trung điểm của EC Gọi ([tex]\alpha[/tex]) là mặt phẳng chứa AE và // với BD
a, xác định thiết diện của hình chóp cắt bới mặt phẳng ([tex]\alpha[/tex])
b, Gọi P là điểm bất kì thuộc cạnh BD . Chứng minh FP // với ([tex]\alpha[/tex])
c, tính diện tích ở câu a,