View attachment 175072
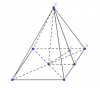
$S.ABCD$ là hình chóp đều $=> CD//AB$
$(SAB)$ chứa $SA, AB=> d(CD,SA)=d(CD,(SAB))=d(C,(SAB))$
Ta có: $OA=\frac{1}{2}.AC=> d(C,(SAB))=2.d(O,(SAB))$
Từ $O$ kẻ $OE \perp AB=> E$ là trung điểm $AB=>SE \perp AB$.
[tex]\left\{\begin{matrix} SO \perp AB & \\ OE \perp AB & \\ SO \cap OE=O & \end{matrix}\right.=>AB \perp (SOE)=> (SAB)\perp(SOE)[/tex]
Trong mp' $(SOE)$ ,từ $O$ kẻ $OF \perp SE$
$=> OF=d(O,(SAB))$
Theo bài ra $d(CD,SA)=SO=>SO=2.OF$
$\Delta SOF$ vuông tại $F$, $SO=2OF=>\widehat{OSF}=30^o=> \widehat{SEO}=60^o$.
$=> SE=2OE=2.\frac{a}{2}=a$
$=> SO=SE.sin60^o=\frac{a\sqrt{3}}{2}$
Áp dụng định lý Pytago đối với $\Delta SEA$:
$SA=\sqrt{a^2+(\frac{a}{2})^2}=\frac{a\sqrt{5}}{2}$
$=> sin \widehat{SAO}=\frac{SO}{SA}=\frac{\frac{a\sqrt{3}}{2}}{\frac{a\sqrt{5}}{2}}=\frac{\sqrt{15}}{5}$
Chọn B ạ :vv
(Ế cái hình bị lỗi mất cái cạnh DC rùi :>)
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
