[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Bài 1 Cho ∆ABC có 3 góc nhọn .Các đường cao AD ,BE,CF. CM
a) ∆AEB~∆AFC; ∆AEF~∆ABC
b)S∆DEF/S∆ABC= 1-(cos^2A+cos^2B+cos^2C)
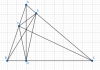
Bài 2: Cho đoạn thẳng AB.Trên cùng một nửa mặt phẳng bờ là AB vẽ tia Ax ,By vuông góc với AB.Gọi O là trung điểm của AB.Trên tia Ax lấy D ,tia By lấy C sao cho AD<BC và góc COD=90°.Hai đường thẳng AB và CD cắt nhau tại E.Từ O kẻ OH vuông góc CD(H thuộc CD).CMR
a)OC^2.DH=OD^2.CH
b) DO là tia phân giác góc ADC
b) AH^2/BH^2= AE/BE
Các bn làm nhanh giúp mik vs nhá vì sớm nay mik fai nộp rôi
.thanks các bn nhiều☺☺☺☺
a) ∆AEB~∆AFC; ∆AEF~∆ABC
b)S∆DEF/S∆ABC= 1-(cos^2A+cos^2B+cos^2C)
Bài 2: Cho đoạn thẳng AB.Trên cùng một nửa mặt phẳng bờ là AB vẽ tia Ax ,By vuông góc với AB.Gọi O là trung điểm của AB.Trên tia Ax lấy D ,tia By lấy C sao cho AD<BC và góc COD=90°.Hai đường thẳng AB và CD cắt nhau tại E.Từ O kẻ OH vuông góc CD(H thuộc CD).CMR
a)OC^2.DH=OD^2.CH
b) DO là tia phân giác góc ADC
b) AH^2/BH^2= AE/BE
Các bn làm nhanh giúp mik vs nhá vì sớm nay mik fai nộp rôi
.thanks các bn nhiều☺☺☺☺