M
myhairone
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
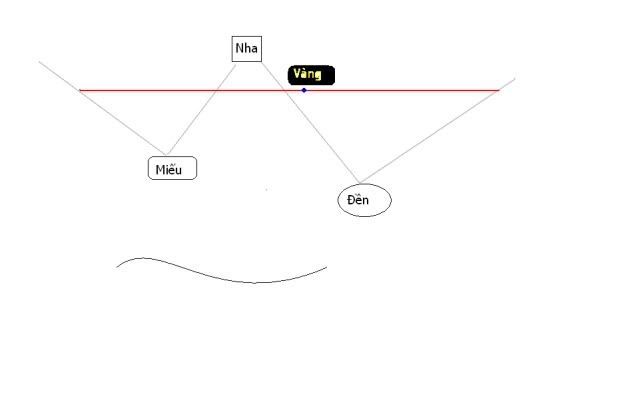
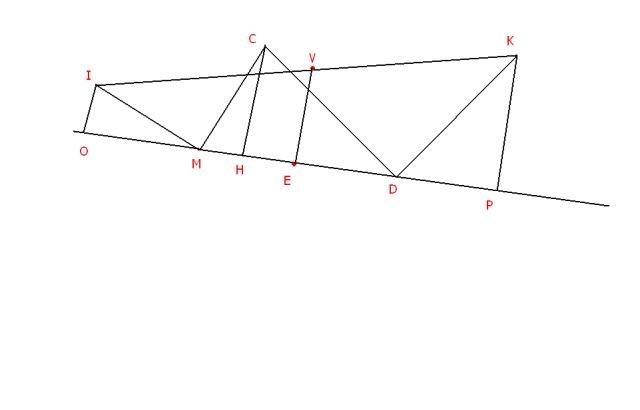
Vào 50 năm trước, có 1 ông già cả đời chỉ dành dụm tiền nuôi các con. Vào 1 hôm, Trung Quốc sang xâm lược nước ta. Ông ta biết chắc sẽ phải trốn đi nên dấu số tiền dành dụm cả đời đó đi. Ông ta không dấu ở nhà vì sợ sẽ bị tìm ra nên ông đã đi ra 1 con đê cách nhà khá xa. Xa xa ông thấy một cây cổ thụ rất to, bên tay phải ông là 1 cái miếu còn bên trái là 1 cái đền. Ông ra chỗ cây to. Từ cây to ông đi vài bước ra chỗ cái miếu, rồi ông đi vuông góc với đoạn đường vừa nãy cùng với ngần ấy bước. Tương tự với đường đi từ cây ra đền. Ông lấy 1 đoạn dây thừng, 1 đầu là điểm đến của đường vuông góc với miếu còn 1 đàu là điểm đến của đường vuông góc với đền. Sau đó ông ý lấy trung điẻm của đoạn dây rồi gấp đôi dây lại. Đó chính là nơi ông dấu vàng. Ông ghi lại vào 1 mảnh giấy. Rồi ông đến 1 nơi rất xa, sinh con đẻ cái ... 50 năm sau, ông đưa mảnh giáy đó cho con mình bảo con ra chỗ ông dấu vàng để đào lên nhưng nơi đó đã trở nên hoàn toàn khác. Nơi cây to thì đã mọc lên những xí nghiệp nhà máy. Nhưng ngôi miếu và ngôi đền thì không bị thay đổi. Làm thế nào để tìm ra nơi cất dấu vàng. Đó vẫn chỉ là dấu ?????? Hãy giúp mình nha!! thank trước nha.
Last edited by a moderator: