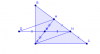
Trên tia đối của MN, vẽ D sao cho DM = MN
Xét △△ \triangle DMH và △△ \triangle NMA ta có:
DM = MN (gt)
DMHˆ=
NMAˆDMH^=NMA^ \widehat{DMH} = \widehat{NMA} (đối đỉnh)
MH = MA (gt)
⇒△⇒△ \Rightarrow \triangle DMH = △△ \triangle NMA (c.g.c)
⇒
HDNˆ=
ANDˆ⇒HDN^=AND^ \Rightarrow \widehat{HDN} = \widehat{AND} (góc tương ứng) và DH = AN (cạnh tương ứng)
Mà
HDNˆHDN^ \widehat{HDN} và
ANDˆAND^ \widehat{AND} nằm ở vị trí so le trong
⇒⇒ \Rightarrow DH // AN
⇒
DHNˆ=
ANCˆ⇒DHN^=ANC^ \Rightarrow \widehat{DHN} = \widehat{ANC}
Xét △△ \triangle DHN và △△ \triangle ANC ta có:
DH = AN (cmt)
DHNˆ=
ANCˆDHN^=ANC^ \widehat{DHN} = \widehat{ANC} (cmt)
HN = NC (gt)
⇒△⇒△ \Rightarrow \triangle DHN = △△ \triangle ANC (c.g.c)
⇒
HNDˆ=
NCAˆ⇒HND^=NCA^ \Rightarrow \widehat{HND} = \widehat{NCA} (góc tương ứng) và DN = AC (cạnh tương ứng)
a.
HNDˆ=
NCAˆHND^=NCA^ \widehat{HND} = \widehat{NCA} (cmt) mà
HNDˆHND^ \widehat{HND} và
NCAˆNCA^ \widehat{NCA} nằm ở vị trí đồng vị
⇒
ND//
AC⇒ND//AC \Rightarrow ND // AC
b. Ta có: DM + MN = DN
Mà DM = MN (gt)
⇒⇒ \Rightarrow 2 MN = DN
Mà DN = AC (cmt)
⇒⇒ \Rightarrow 2MN = AC
⇒⇒ \Rightarrow MN = 1212 \frac12 AC
PS: Mk thấy nó hơi dài, k bt có cách nào ngắn hơn k, mk k giỏi lắm phần Hình, bn thông cảm.
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.