Cho tam giác ABC có góc B bằng góc C, kẻ AH vuông góc với BC, H thuộc BC. Trên tia đối của tia BC lấy điểm D. Trên tia đối của tia CB lấy điểm E sao cho BD = CE. Chứng minh:
a) AB = AC
b) Tam giác ABD bằng tam giác ACE
c) Tam giác ACD bằng tam giác ABE
d) AH là tia phân giác của góc DAE
e) Kẻ BK vuông góc với AD, CI vuông góc với AE. Chứng minh ba đường thẳng AH, BK cùng đi qua một điểm
Lưu ý: Em chưa học bài đồng quy nên đừng lôi nó vào ạ, nếu có thì hãy chứng minh trước rồi làm nhé!
-Ta có: [tex]\widehat{B}=\widehat{C}\left ( gt \right )[/tex]
[tex]\widehat{H}=90^{\circ}[/tex]
[tex]\Rightarrow\widehat{BAH}=\widehat{CAH}[/tex]
a,-Xét [tex]\Delta ABH và \Delta ACH[/tex] có:
+[tex]AH[/tex] là cạnh chung
+[tex]\widehat{BAH}=\widehat{CAH}\left ( cmt \right )[/tex]
+[tex]\widehat{AHB}=\widehat{AHC}\left ( \widehat{H}=90^{\circ} \right )[/tex]
-Suy ra:[tex]\Delta ABH=\Delta ACH\left ( g-c-g \right )[/tex]
b,-Ta có: +[tex]\widehat{ABD}+\widehat{ABH}=180^{\circ}[/tex]
+ [tex]\widehat{ACE}+\widehat{ACH}=180^{\circ}[/tex]
-Mà [tex]\widehat{ABH}=\widehat{ACH}\left ( gt \right )[/tex]
-Nên:[tex]\widehat{ABD}=\widehat{ACE}\left ( ....\right )[/tex]
-Xét [tex]\Delta ABD và \Delta ACE[/tex] có:
+[tex]\widehat{ABD}=\widehat{ACE}\left ( cmt \right )[/tex]
+[tex]AB=AC\left ( 2 cạnh tương ứng \right )[/tex]
+[tex]\widehat{DAB}=\widehat{CAE}\left (bạn tự c/m như trên \right )[/tex]
-Vậy: [tex]\Delta ABD=\Delta ACE\left ( g-c-g \right )[/tex]
c,-Xét: [tex]\Delta ADC và \Delta ABE có:[/tex]
+[tex]DE là cạnh chung[/tex]
+[tex]\widehat{D}=\widehat{E}\left ( 2 góc tương ứng \right )[/tex]
+[tex]\widehat{ABH}=\widehat{ACH}\left ( gt \right )
-Vậy: [tex]\Delta ADC =\Delta ABE\left ( g-c-g \right )[/tex]
4.-Xét:[tex]\Delta ADH và \Delta AEH có:[/tex]
+[tex]AD=AE\left ( 2 cạnh tương ứng \right )[/tex]
+[tex]\widehat{D}=\widehat{E}\left ( góc tương ứng \right )[/tex]
+[tex]DB=CE\left ( gt \right )[/tex]
-Suy ra: [tex]\Delta ADH=\Delta AEH\left ( c-g-c \right )[/tex]
[tex]\Rightarrow \widehat+{DAH}=\widehat{EAH}\left ( 2 góc tương ứng \right )[/tex]
-Vậy: AH là tia phân giác [tex]\widehat{DAE}[/tex] (đpcm).
e,e) Kẻ BK vuông góc với AD, CI vuông góc với AE. Chứng minh ba đường thẳng AH, BK cùng đi qua một điểm đề thiếu nhé bạn.....\
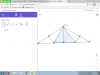
Quên mất cái hình, đây:
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
