[Hình học 7]Một bài toán hình khó

[thinh25129]

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

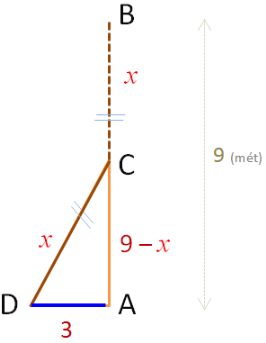
Một cái cây cao 9m bị gãy một đoạn ở giữa, ngọn cây xà xuống đất, biết từ ngọn cây đến gốc cây là 3m hỏi độ dài từ chỗ bị gãy đến gốc cây là bao nhiêu mét ?

 

[me0kh0ang2000]

Gọi đoạn từ chỗ bị gãy đến ngọn cây là x. do đó, từ chỗ bị gãy đến ngọn cây và đến phần cách gốc 3m, nơi ngọn cây khi gãy xuống chạm vào sẽ bằng nhau, hay 2x.

ta có:
2x + 3 = 9 \Rightarrow x = 3

Vậy, từ chỗ bị gãy đến gốc cây là:
3+3 = 6 (m)

 

[thinhrost1]

Gọi đoạn từ chỗ bị gãy đến ngọn cây là x. do đó, từ chỗ bị gãy đến ngọn cây và đến phần cách gốc 3m, nơi ngọn cây khi gãy xuống chạm vào sẽ bằng nhau, hay 2x.

ta có:
2x + 3 = 9 \Rightarrow x = 3

Vậy, từ chỗ bị gãy đến gốc cây là:
3+3 = 6 (m)

Mình có cách này:
Cái cây cao 9m chỗ gãy đến ngọn cây là 3m. Vậy chỗ bị gẫy đến gốc cây là:
9-3=6(m)
Không cần làm dài dòng cho mệt 8-}

 

[thinh25129]

K đơn giản như thế đâu pn

Gọi đoạn từ chỗ bị gãy đến ngọn cây là x. do đó, từ chỗ bị gãy đến ngọn cây và đến phần cách gốc 3m, nơi ngọn cây khi gãy xuống chạm vào sẽ bằng nhau, hay 2x.

ta có:
2x + 3 = 9 \Rightarrow x = 3

Vậy, từ chỗ bị gãy đến gốc cây là:
3+3 = 6 (m)

Chắc pn nhầm lẫn gì rồi
Cho cái cây là 1 đoạn thẳng AB dài 9m. Nhưng bị gãy ở giữa, tại điểm C. Vì bị gãy nên ngọn cây, chỗ điểm B bị xòa xuống đất chỗ điểm D. Ta có A, C, D tạo thành tam giác vuông tại A với cạch AD dài 3m và BC=BD
Bạn có thể lm với gợi ý này sử dụng định lý Pytago, mk thì đã bí rồi.

 

[0973573959thuy]

Chắc pn nhầm lẫn gì rồi
Cho cái cây là 1 đoạn thẳng AB dài 9m. Nhưng bị gãy ở giữa, tại điểm C. Vì bị gãy nên ngọn cây, chỗ điểm B bị xòa xuống đất chỗ điểm D. Ta có A, C, D tạo thành tam giác vuông tại A với cạch AD dài 3m và BC=BD
Bạn có thể lm với gợi ý này sử dụng định lý Pytago, mk thì đã bí rồi.

Sao bạn biết BC = BD :-SS
Xét tam giác BAD vuông tại A.
Theo định lý Py - ta - go ta tính được BD xấp xỉ 9,4 lớn hơn đoạn BA = 9 (1)
Mà c nằm giữa A,B nên BC < BA (2)
Từ (1); (2) \Rightarrow $BD \not= BC$
Vậy bạn nói sai.

 

[soicon_boy_9x]

Các bạn làm sai rồi

Nhìn hình vẽ này

Đặt gốc cây là A, chỗ gãy là O, ngọn cây là B

Ta có:

$AO+OB=9 \rightarrow x+y=9(1)$ và $AB=3$

Áp dụng định lý Py-ta-go vào tam giác $AOB$ vuông tại A ta được:

$OB^2-OA^2=AB^2$

$\rightarrow y^2-x^2=9$

$\rightarrow y^2-xy+xy-y^2=9 \rightarrow y(y-x)+x(y-x)=9 \rightarrow
(x+y)(y-x)=9$

Thay $x+y=9$ ta được:

$9(y-x)=9 \rightarrow y-x=1(2)$

Từ (1) và (2) $\rightarrow y=5;x=4$

Vậy khoảng cách từ chỗ gãy đến gốc cây là 4m

 

[sieumau88]

Chắc pn nhầm lẫn gì rồi
Cho cái cây là 1 đoạn thẳng AB dài 9m. Nhưng bị gãy ở giữa, tại điểm C. Vì bị gãy nên ngọn cây, chỗ điểm B bị xòa xuống đất chỗ điểm D. Ta có A, C, D tạo thành tam giác vuông tại A với cạch AD dài 3m và BC=BD
Bạn có thể lm với gợi ý này sử dụng định lý Pytago, mk thì đã bí rồi.

___________________

Sao bạn biết BC = BD :-SS
Xét tam giác BAD vuông tại A.
Theo định lý Py - ta - go ta tính được BD xấp xỉ 9,4 lớn hơn đoạn BA = 9 (1)
Mà c nằm giữa A,B nên BC < BA (2)
Từ (1); (2) \Rightarrow $BD \not= BC$
Vậy bạn nói sai.

________

Ah` thiệt ra là bạn Thinh25129 viết nhầm BD = BC \Rightarrow sửa lại là BC = CD

Vì $\Delta ACD$ vuông tại A
nên $CD^2 = AD^2 + AC^2$
$x^2 = 3^2 + \left(9-x \right)^2$
$x = 5$
Vậy, từ chỗ bị gãy đến gốc cây là $CA = 9 - 5 = 4$ (mét)

 

[thinh25129]

ồ, mk nhầm

Sao bạn biết BC = BD :-SS
Xét tam giác BAD vuông tại A.
Theo định lý Py - ta - go ta tính được BD xấp xỉ 9,4 lớn hơn đoạn BA = 9 (1)
Mà c nằm giữa A,B nên BC < BA (2)
Từ (1); (2) \Rightarrow $BD \not= BC$
Vậy bạn nói sai.

ồ ! xin lỗi , mình đánh nhầm phải là BC=CD mới đúng . Hì

 

[thinh25129]

mk chưa hỉu

___________________



________

Ah` thiệt ra là bạn Thinh25129 viết nhầm BD = BC \Rightarrow sửa lại là BC = CD

Vì $\Delta ACD$ vuông tại A
nên $CD^2 = AD^2 + AC^2$
$x^2 = 3^2 + \left(9-x \right)^2$
$x = 5$
Vậy, từ chỗ bị gãy đến gốc cây là $CA = 9 - 5 = 4$ (mét)

Từ phần:

$x^2 = 3^2 + \left(9-x \right)^2$
$x = 5$
mk vẫn chưa hiểu pn tính như thế nào

 

[thinh25129]

Các bạn làm sai rồi

Nhìn hình vẽ này

Đặt gốc cây là A, chỗ gãy là O, ngọn cây là B

Ta có:

$AO+OB=9 \rightarrow x+y=9(1)$ và $AB=3$

Áp dụng định lý Py-ta-go vào tam giác $AOB$ vuông tại A ta được:

$OB^2-OA^2=AB^2$

$\rightarrow y^2-x^2=9$

$\rightarrow y^2-xy+xy-y^2=9 \rightarrow y(y-x)+x(y-x)=9 \rightarrow
(x+y)(y-x)=9$

Thay $x+y=9$ ta được:

$9(y-x)=9 \rightarrow y-x=1(2)$

Từ (1) và (2) $\rightarrow y=5;x=4$

Vậy khoảng cách từ chỗ gãy đến gốc cây là 4m

Mình cũng nhẫm được bằng 4m nhưng không biết cách làm cảm ơn bạn nhiều nha