Toán 9 hình 9

[huubay]

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

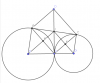
Cho hai đường tròn tâm $(O)$ và $(O')$ tiếp xúc ngoài tại $A$. Kẻ tiếp tuyến chung ngoài $BC$, $B \in (O)$, $C \in (O')$. Tiếp tuyến chung trong tại $A$ cắt tiếp tuyến chung ngoài $BC$ tại $I$.
a, Cminh $\widehat{BAC}=90^{\circ}$.
b, Trên tia đối của tía $IA$ lấy điểm $D$ sao cho $IA=ID$. Tứ giác $ABDC$ là hình gì, vì sao?
c, Gọi giao điểm của $OI$ và $AB$ là $M$; giao điểm của $O'I$ và $AC$ là $N$, chứng minh rằng $\dfrac{OM}{O'N}=\dfrac{OI^3}{O'I^3}$

 

[Ann Lee]

Câu c)
Xét [tex]\Delta IOO'[/tex] vuông tại I ( dễ c/m), đường cao $IA$
$OI^{2}=OA.OO';O'I^{2}=O'A.OO'$ (hệ thức giữa cạnh và đường cao trong tam giác vuông)
$\Rightarrow \frac{OA}{O'A}=\frac{OI^{2}}{O'I^{2}}\Leftrightarrow \frac{OA^{2}}{O'A^{2}}=\frac{OI^{4}}{O'I^{4}}$ (1)
Xét $\Delta IAO$, đường cao $AM$ (dễ c/m) có:
[tex]OA^{2}=OI.OI[/tex] (hệ thức giữa cạnh và đường cao trong tam giác vuông)
Xét $\Delta IAO'$, đường cao $AM$ (dễ c/m) có:
[tex]O'A^{2}=O'I.O'N[/tex] (hệ thức giữa cạnh và đường cao trong tam giác vuông)
Suy ra [tex]\frac{OA^{2}}{O'A^{2}}=\frac{OM.OI}{O'N.O'I}[/tex] (2)
Từ (1) và (2) suy ra [tex]\frac{OM.OI}{O'N.O'I}=\frac{OI^{4}}{O'I^{4}}\Leftrightarrow \frac{OM}{O'N}=\frac{OI^{3}}{O'I^{3}}[/tex] (đpcm)