- 15 Tháng chín 2017
- 193
- 77
- 69
- Thái Nguyên
- THPT Điềm Thụy
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
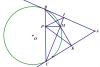
Câu 7: Từ 1 điểm A nằm ngoài đường tròn (O;R) ta vẽ hai tiếp tuyến AB, AC với đường tròn (B;C tiếp điểm). Trên cung nhỏ BC lấy một điểm M, vẽ MI vuông góc AC (I thuộc AB, K thuộc AC)
Vẽ MP vuông góc BC (P thuộc BC). Chứng minh gócMPK = gócMBC
Xác định vị trí của điểm M trên cung nhỏ BC để tích MI.MK.MP đạt giá trị lớn nhất
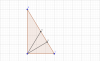
Câu 8: Trong tam giác vuông, tỉ số giữa đường cao và đường trung tuyến kẻ từ đỉnh góc vuông bằng 40:41. Tính độ dài các cạnh góc vuông bằng 40:41. Tính độ dài các cạnh góc vuông của tam giác, biết cạnh huyền bằng căn41 cm
Vẽ MP vuông góc BC (P thuộc BC). Chứng minh gócMPK = gócMBC
Xác định vị trí của điểm M trên cung nhỏ BC để tích MI.MK.MP đạt giá trị lớn nhất
Câu 8: Trong tam giác vuông, tỉ số giữa đường cao và đường trung tuyến kẻ từ đỉnh góc vuông bằng 40:41. Tính độ dài các cạnh góc vuông bằng 40:41. Tính độ dài các cạnh góc vuông của tam giác, biết cạnh huyền bằng căn41 cm