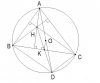
Gọi D là giao điểm của OA và (O)
(O) có [TEX]OK \perp BC \Rightarrow[/TEX] K là trung điểm của BC (định lý)
Ta có:
[tex]\Delta ACD[/tex] nội tiếp (O) có AD là đường kính (cv) [tex]\Rightarrow \Delta ACD[/tex] vuông tại C (định lý) [tex]\Rightarrow AC \perp CD[/tex]
Và [tex]\Delta ABD[/tex] nội tiếp (O) có AD là đường kính (cv) [tex]\Rightarrow \Delta ABD[/tex] vuông tại C (định lý) [tex]\Rightarrow AB \perp BD[/tex]
Mà [TEX]BH \perp AC[/TEX] và [TEX]CH \perp AB[/TEX] (gt)
Nên BH // CD và CH // BD
[TEX]\Rightarrow[/TEX] Tứ giác BHCD là hình bình hành có K là trung điểm của BC (cmt)
[TEX]\Rightarrow[/TEX] K là trung điểm của HD.
[tex]\Delta AHD[/tex] có O là trung điểm của AD (cv) và K là trung điểm của HD (cmt)
[TEX]\Rightarrow[/TEX] OK là đường trung bình của [tex]\Delta AHD[/tex]
[TEX]\Rightarrow[/TEX] AH = 2OK
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
