Hình 8 cần gấp

[Nguỵ Quân Tử]

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

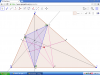
Cho tam giác ABC nhọn. Các đường cao AD, BE, CF cắt nhau tại H.

a) Chứng minh rằng: BD.DC=DH.DA.

b) CMR: [tex]\frac{HD}{AD} + \frac{HE}{BE} + \frac{HF}{CF} = 1[/tex]

c) CMR: H là giao điểm các đường phân giác của tam giác DEF.

d) Gọi M, N, P, Q, I, K lần lượt là trung điểm của các đoạn thẳng BC, CA, AB, EF, FD, DE.CMR: MQ, NI, PK đồng quy tại 1 điểm.

Mấy bạn giúp mình phần c,d nha, mình mới làm được a,b

 

[Nguyễn Xuân Hiếu]

c)Ta có :
[tex]\triangle BDA \sim \triangle BFC \\\Rightarrow \frac{BD}{BF}=\frac{BA}{BC} \\\Rightarrow \triangle BFD \sim \triangle BCA(c.g.c) \\\Rightarrow \widehat{BFD}=\widehat{BCA}[/tex]
Chứng minh tương tự

[tex]\Rightarrow \widehat{AFE}=\widehat{ACB} \\\Rightarrow \widehat{AFE}=\widehat{BFD} \\\widehat{BFD}+\widehat{DFC}=90^0 \\\widehat{AFE}+\widehat{EFC}=90^0 \\\Rightarrow \widehat{DFC}=\widehat{EFC}[/tex]
Từ đó có FH là tia phân giác $\widehat{EFD}$.
Chứng minh tương tự ta sẽ có điều phải chứng minh .
d)Ta có:$EM,FM$ là đường trung tuyến ứng với cạnh huyền $BC$.
$\Rightarrow FM=EM$.
Mà $Q$ là trung điểm của $EF$.
$\Rightarrow QM$ là đường trung trực $\triangle DEF$.
Chứng minh tương tự sẽ được $PK,NI$ cũng là đường trung trực nên chúng đồng quy.