S
shjnjchjkudo96
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Trong toán học, định lý Pytago (còn gọi là định lý Pythagore theo tiếng Pháp hay định lý Pythagoras theo tiếng Anh) là một liên hệ trong hình học phẳng giữa ba cạnh của một tam giác vuông.
Định lý này được đặt tên theo nhà triết học và nhà toán học Hy Lạp Pytago sống vào thế kỷ 6 TCN, mặc dù định lý toán học này đã được biết đến bởi các nhà toán học Ấn Độ (trong quyển Sulbasutra của Baudhayana và Katyayana), Hy Lạp, Trung Quốc và Babylon từ nhiều thế kỷ trước.
Hai cách chứng minh cổ nhất của định lý Pytago được cho là nằm trong quyển Chu bễ toán kinh (周髀算经) khoảng năm 500 đến 200 TCN và Các nguyên tố của Euclid khoảng 300 năm TCN.
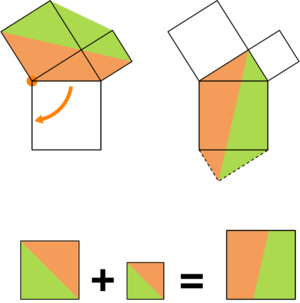
Có hàng nghìn cách chứng minh định lý Pytago. Cách chứng minh được thể hiện trong hình này thuộc về Leonardo da Vinci[/font]
Định lý
Cách phát biểu của Euclid:
Tổng diện tích của hai hình vuông vẽ trên cạnh kề của một tam giác vuông bằng diện tích hình vuông vẽ trên cạnh huyền của tam giác này.
Một tam giác vuông là một tam giác có một góc vuông; các cạnh kề của nó là các cạnh tạo nên góc vuông; cạnh huyền là cạnh đối diện với góc vuông. Trong hình vẽ dưới, a và b là các cạnh kề, c là cạnh huyền:
Pytago đã phát biểu định lý mang tên ông trong cách nhìn của hình học phẳng thông qua:
Diện tích hình vuông tím bằng tổng diện tích hình vuông đỏ và xanh lam.
Tương tự, quyển Sulbasutra chép:
Một dây thừng nối dọc đường chéo hình chữ nhật tạo ra một diện tích bằng tổng diện tích tạo ra từ cạnh ngang và cạnh dọc của hình chữ nhật đó.
Dùng đại số sơ cấp hay hình học đại số, có thể viết định lý Pytago dưới dạng hiện đại, chú ý rằng diện tích một hình vuông bằng bình phương độ dài của cạnh hình vuông đó:
Nếu một tam giác vuông có cạnh kề dài bằng a và b và cạnh huyền dài c, thì [tex]a^2 + b^2 = c^2[/tex]
Định lý đảo
Định lý đảo Pytago phát biểu là:
Cho ba số thực dương a, b, và c thỏa mãn [tex]a^2 + b^2 = c^2[/tex], tồn tại một tam giác có các cạnh là a, b và c, và góc giữa a và b là một góc vuông.
Định lý đảo này cũng xuất hiện trong quyển Các nguyên tố và được phát biểu bởi Euclid là:
Nếu bình phương của một cạnh của một tam giác bằng tổng bình phương hai cạnh kia, thì tam giác có góc nằm giữa hai cạnh nhỏ là góc vuông.
Bộ ba Pytago
Tập hợp các số a, b và c thỏa mãn [tex]a^2 + b^2 = c^2[/tex] được gọi là bộ ba Pytago. Trong lịch sử, người ta thường quan tâm tới các bộ ba này với a, b và c là các số nguyên. Ví dụ {3, 4, 5} hay tổng quát hơn, bộ các số [tex]a, b = \frac{a^2-1}{2}, c = \frac{a^2+1}{2}[/tex] được những người thuộc trường phái Pytago khám phá ra cũng thỏa mãn phương trình này
http://www.cut-the-knot.org/pythagoras/index.shtml
Hơn 50 cách chứng minh cho định lý Pitago
Định lý này được đặt tên theo nhà triết học và nhà toán học Hy Lạp Pytago sống vào thế kỷ 6 TCN, mặc dù định lý toán học này đã được biết đến bởi các nhà toán học Ấn Độ (trong quyển Sulbasutra của Baudhayana và Katyayana), Hy Lạp, Trung Quốc và Babylon từ nhiều thế kỷ trước.
Hai cách chứng minh cổ nhất của định lý Pytago được cho là nằm trong quyển Chu bễ toán kinh (周髀算经) khoảng năm 500 đến 200 TCN và Các nguyên tố của Euclid khoảng 300 năm TCN.
Có hàng nghìn cách chứng minh định lý Pytago. Cách chứng minh được thể hiện trong hình này thuộc về Leonardo da Vinci
Định lý
Cách phát biểu của Euclid:
Tổng diện tích của hai hình vuông vẽ trên cạnh kề của một tam giác vuông bằng diện tích hình vuông vẽ trên cạnh huyền của tam giác này.
Một tam giác vuông là một tam giác có một góc vuông; các cạnh kề của nó là các cạnh tạo nên góc vuông; cạnh huyền là cạnh đối diện với góc vuông. Trong hình vẽ dưới, a và b là các cạnh kề, c là cạnh huyền:
Diện tích hình vuông tím bằng tổng diện tích hình vuông đỏ và xanh lam.
Tương tự, quyển Sulbasutra chép:
Một dây thừng nối dọc đường chéo hình chữ nhật tạo ra một diện tích bằng tổng diện tích tạo ra từ cạnh ngang và cạnh dọc của hình chữ nhật đó.
Dùng đại số sơ cấp hay hình học đại số, có thể viết định lý Pytago dưới dạng hiện đại, chú ý rằng diện tích một hình vuông bằng bình phương độ dài của cạnh hình vuông đó:
Nếu một tam giác vuông có cạnh kề dài bằng a và b và cạnh huyền dài c, thì [tex]a^2 + b^2 = c^2[/tex]
Định lý đảo
Định lý đảo Pytago phát biểu là:
Cho ba số thực dương a, b, và c thỏa mãn [tex]a^2 + b^2 = c^2[/tex], tồn tại một tam giác có các cạnh là a, b và c, và góc giữa a và b là một góc vuông.
Định lý đảo này cũng xuất hiện trong quyển Các nguyên tố và được phát biểu bởi Euclid là:
Nếu bình phương của một cạnh của một tam giác bằng tổng bình phương hai cạnh kia, thì tam giác có góc nằm giữa hai cạnh nhỏ là góc vuông.
Bộ ba Pytago
Tập hợp các số a, b và c thỏa mãn [tex]a^2 + b^2 = c^2[/tex] được gọi là bộ ba Pytago. Trong lịch sử, người ta thường quan tâm tới các bộ ba này với a, b và c là các số nguyên. Ví dụ {3, 4, 5} hay tổng quát hơn, bộ các số [tex]a, b = \frac{a^2-1}{2}, c = \frac{a^2+1}{2}[/tex] được những người thuộc trường phái Pytago khám phá ra cũng thỏa mãn phương trình này
[Bài viết từ wikipedia]
http://www.cut-the-knot.org/pythagoras/index.shtml
Hơn 50 cách chứng minh cho định lý Pitago
