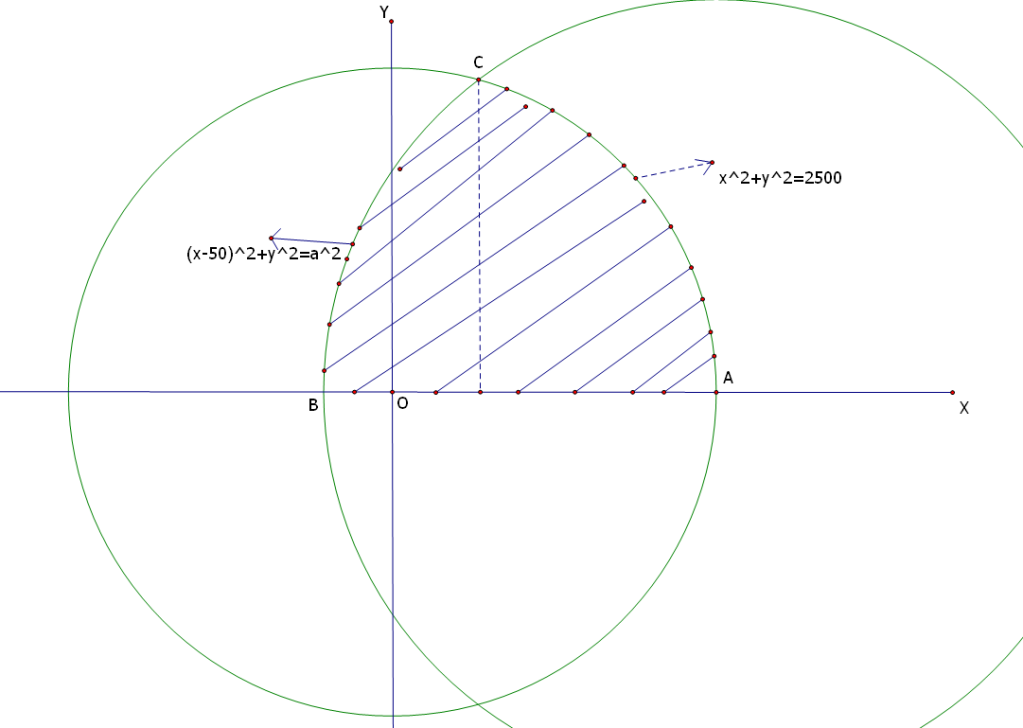
có 1 đám cỏ hình tròn, bán kính 50m. 1 cái cọc cắm ở mép đường tròn (ngoài lề đám cỏ đó). hỏi cột con bò bằng sợi dây dài ? để nó ăn dược 1/2 diiện tích đám cỏ?
[TEX]\int\limits_a^b {\sqrt {{\alpha ^2} - {x^2}} } = \frac{{x\sqrt {{\alpha ^2} - {x^2}} }}{2} + \frac{{{\alpha ^2}}}{2}\arcsin \frac{x}{\alpha }[/TEX]
[TEX]{\rm{0 < y < 50}}{\rm{, - 50}} \le {\rm{x}} \le {\rm{50}}[/TEX]
[TEX]\begin{array}{l}{x^2} + {y^2} = 2500 \Rightarrow y = \sqrt {2500 - {x^2}} \\ {(x - 50)^2} + {y^2} = {a^2}{\rm{ (0 < a < 100)}} \Rightarrow {\rm{y = }}\sqrt{{a^2} - {{(x - 50)}^2}} \\ \sqrt {2500 - {x^2}} = \sqrt {{a^2} - {{(x - 50)}^2}} \Leftrightarrow x = 50-\frac{{{a^2}}}{{100}} \\ \end{array}[/TEX]
[TEX]\begin{array}{l}S = \int\limits_{50 - a}^{50} {\left| {\sqrt {{a^2} - {{(x - 50)}^2}} - \sqrt {2500 -{x^2}} } \right|} dx = \int\limits_{50 - a}^{50 - \frac{{{a^2}}}{{100}}} {\left({\sqrt {2500 - {x^2}} - \sqrt {{a^2} - {{(x - 50)}^2}} } \right)dx} \\ + \int\limits_{50 - \frac{{{a^2}}}{{100}}}^{50} {\left( {\sqrt {{a^2} - {{(x -50)}^2}} - \sqrt {2500 - {x^2}} } \right)} dx = \int\limits_{50 - a}^{50 -\frac{{{a^2}}}{{100}}} {\sqrt {2500 - {x^2}} dx} - \int\limits_{50 - a}^{50 - \frac{{{a^2}}}{{100}}} {\sqrt {{a^2} - {{(x - 50)}^2}} dx} \\ + \int\limits_{50 - \frac{{{a^2}}}{{100}}}^{50} {\sqrt {{a^2} - {{(x - 50)}^2}}} dx - \int\limits_{50 - \frac{{{a^2}}}{{100}}}^{50} {\sqrt {2500 - {x^2}} } dx =A - B + C - D \\ \end{array}[/TEX]
[TEX]\begin{array}{l}A = \int\limits_{50 - a}^{50 - \frac{{{a^2}}}{{100}}} {\sqrt {2500 - {x^2}} dx} = \left( {\frac{{x\sqrt {{{50}^2} - {x^2}} }}{2} + \frac{{{{50}^2}}}{2}\arcsin \frac{x}{{50}}} \right)\left| \begin{array}{l}50 - \frac{{{a^2}}}{{100}} \\ 50 - a \\\end{array} \right. = \\ \left( {\frac{{\left( {50 - \frac{{{a^2}}}{{100}}} \right)\sqrt {{{50}^2} - {{\left( {50 - \frac{{{a^2}}}{{100}}} \right)}^2}} }}{2} + \frac{{{{50}^2}}}{2}\arcsin \frac{{50 - \frac{{{a^2}}}{{100}}}}{{50}}} \right) - \\ \left( {\frac{{\left( {50 - a} \right)\sqrt {{{50}^2} - {{\left( {50 - a} \right)}^2}} }}{2} + \frac{{{{50}^2}}}{2}\arcsin \frac{{50 - a}}{{50}}} \right) = \\ \left( {\left( {25 - \frac{{{a^2}}}{{200}}} \right)\sqrt {{a^2} - \frac{{{a^4}}}{{10000}}} + \frac{{{{50}^2}}}{2}\arcsin \left( {1 - \frac{{{a^2}}}{{5000}}} \right)} \right) - \\ \left( {\left( {25 - \frac{a}{2}} \right)\sqrt {100a - {a^2}} + 1250\arcsin \left( {1 - \frac{a}{{50}}} \right)} \right) \\ \end{array}[/TEX]
[TEX]\begin{array}{l}B = \int\limits_{50 - a}^{50 - \frac{{{a^2}}}{{100}}} {\sqrt {{a^2} - {{(x - 50)}^2}} dx} = \int\limits_{ - a}^{ - \frac{{{a^2}}}{{100}}} {\sqrt {{a^2} - {t^2}} dt} = \left( {\frac{{t\sqrt {{a^2} - {t^2}} }}{2} + \frac{{{a^2}}}{2}\arcsin \frac{t}{a}} \right)\left| \begin{array}{l}- \frac{{{a^2}}}{{100}} \\ - a \\ \end{array} \right.(t = x - 50) = \\ \left( {\frac{{\left({-\frac{{{a^2}}}{{100}}} \right)\sqrt {{a^2} - {{\left( { - \frac{{{a^2}}}{{100}}} \right)}^2}} }}{2} + \frac{{{a^2}}}{2}\arcsin \frac{{\left( { - \frac{{{a^2}}}{{100}}} \right)}}{a}} \right) - \underbrace {\left( {\frac{{\left( { - a} \right)\sqrt {{a^2} - {{\left( { - a} \right)}^2}} }}{2} + \frac{{{a^2}}}{2}\arcsin \frac{{\left( { - a} \right)}}{a}} \right)}_{\frac{{ - \pi {a^2}}}{4}} \\ = \left( {\frac{{ - {a^2}}}{{200}}} \right)\sqrt {{a^2} - \frac{{{a^4}}}{{10000}}} + \frac{{{a^2}}}{2}\arcsin \left( {\frac{{ - a}}{{100}}} \right) + \frac{{\pi {a^2}}}{4} \\\end{array}[/TEX]
[TEX]\begin{array}{l}C = \int\limits_{50 - \frac{{{a^2}}}{{100}}}^{50} {\sqrt {{a^2} - {{(x - 50)}^2}} } dx = \int\limits_{ - \frac{{{a^2}}}{{100}}}^{50} {\sqrt {{a^2} - {t^2}} dt} = \left( {\frac{{t\sqrt {{a^2} - {t^2}} }}{2} + \frac{{{a^2}}}{2}\arcsin \frac{t}{a}} \right)\left| \begin{array}{l}50 \\ - \frac{{{a^2}}}{{100}} \\ \end{array} \right.(t = x - 50) \\ = \left( {\frac{{50\sqrt {{a^2} - {{50}^2}} }}{2} + \frac{{{a^2}}}{2}\arcsin \frac{{50}}{a}} \right) - \left( {\frac{{\left( { - \frac{{{a^2}}}{{100}}} \right)\sqrt {{a^2} - {{\left( { - \frac{{{a^2}}}{{100}}} \right)}^2}} }}{2} + \frac{{{a^2}}}{2}\arcsin \frac{{\left( { - \frac{{{a^2}}}{{100}}} \right)}}{a}} \right) = \\ \left( {25\sqrt {{a^2} - {{50}^2}} + \frac{{{a^2}}}{2}\arcsin \frac{{50}}{a}} \right) - \left( {\left( { - \frac{{{a^2}}}{{200}}} \right)\sqrt {{a^2} - \frac{{{a^4}}}{{10000}}} + \frac{{{a^2}}}{2}\arcsin \left( { - \frac{a}{{100}}} \right)} \right) \\ \end{array}[/TEX]
[TEX]\begin{array}{l}D = \int\limits_{50 - \frac{{{a^2}}}{{100}}}^{50} {\sqrt {2500 - {x^2}} } dx = \left( {\frac{{x\sqrt {{{50}^2} - {x^2}} }}{2} + \frac{{{{50}^2}}}{2}\arcsin \frac{x}{{50}}} \right)\left| \begin{array}{l}50 \\ 50 - \frac{{{a^2}}}{{100}} \\ \end{array} \right. = \\ \underbrace {\left( {\frac{{50\sqrt {{{50}^2} - {{50}^2}} }}{2} + \frac{{{{50}^2}}}{2}\arcsin \frac{{50}}{{50}}} \right)}_{ = 625\pi } - \left( {\frac{{\left( {50 - \frac{{{a^2}}}{{100}}} \right)\sqrt {{{50}^2} - {{\left( {50 - \frac{{{a^2}}}{{100}}} \right)}^2}} }}{2} + \frac{{{{50}^2}}}{2}\arcsin \frac{{\left( {50 - \frac{{{a^2}}}{{100}}} \right)}}{{50}}} \right) \\ = 625\pi - \left( {25 - \frac{{{a^2}}}{{200}}} \right)\sqrt {{a^2} - \frac{{{a^4}}}{{10000}}} - 1250\arcsin \left( {1 - \frac{{{a^2}}}{{5000}}} \right) \\ \end{array}[/TEX]
ta cần tìm a để
[TEX]S = \frac{{{{50}^2}\pi }}{2} = 1250\pi [/TEX]
mặt khác
[TEX]\begin{array}{l}S = \left( \begin{array}{l}\left( {\left( {25 - \frac{{{a^2}}}{{200}}} \right)\sqrt {{a^2} - \frac{{{a^4}}}{{10000}}} + \frac{{{{50}^2}}}{2}\arcsin \left( {1 - \frac{{{a^2}}}{{5000}}} \right)} \right) - \\ \left( {\left( {25 - \frac{a}{2}} \right)\sqrt {100a - {a^2}} + 1250\arcsin \left( {1 - \frac{a}{{50}}} \right)} \right) \\ \end{array} \right) \\ - \left( {\left( {\frac{{ - {a^2}}}{{200}}} \right)\sqrt {{a^2} - \frac{{{a^4}}}{{10000}}} + \frac{{{a^2}}}{2}\arcsin \left( {\frac{{ - a}}{{100}}} \right) + \frac{{\pi {a^2}}}{4}} \right) \\ + \left( {\left( {25\sqrt {{a^2} - {{50}^2}} + \frac{{{a^2}}}{2}\arcsin \frac{{50}}{a}} \right) - \left( {\left( { - \frac{{{a^2}}}{{200}}} \right)\sqrt {{a^2} - \frac{{{a^4}}}{{10000}}} + \frac{{{a^2}}}{2}\arcsin \left( { - \frac{a}{{100}}} \right)} \right)} \right) \\ - \left( {625\pi - \left( {25 - \frac{{{a^2}}}{{200}}} \right)\sqrt {{a^2} - \frac{{{a^4}}}{{10000}}} - 1250\arcsin \left( {1 - \frac{{{a^2}}}{{5000}}} \right)} \right) = \\ 50\sqrt {{a^2} - \frac{{{a^4}}}{{10000}}} + \frac{{{{50}^2}}}{2}\arcsin \left( {1 - \frac{{{a^2}}}{{5000}}} \right) - \left( {25 - \frac{a}{2}} \right)\sqrt {100a - {a^2}} \\ - {a^2}\arcsin \left( {\frac{{ - a}}{{100}}} \right) - \frac{{\pi {a^2}}}{4} \\ + 25\sqrt {{a^2} - {{50}^2}} + \frac{{{a^2}}}{2}\arcsin \frac{{50}}{a} \\ - 625\pi \\ \end{array}[/TEX]
Đến đây ta giải phương trình
[TEX]S =\\ 50\sqrt {{a^2} - \frac{{{a^4}}}{{10000}}} + \frac{{{{50}^2}}}{2}\arcsin \left( {1 - \frac{{{a^2}}}{{5000}}} \right) - \left( {25 - \frac{a}{2}} \right)\sqrt {100a - {a^2}} \\ - {a^2}\arcsin \left( {\frac{{ - a}}{{100}}} \right) - \frac{{\pi {a^2}}}{4} \\ + 25\sqrt {{a^2} - {{50}^2}} + \frac{{{a^2}}}{2}\arcsin \frac{{50}}{a} \\ - 625\pi = 1250\pi [/TEX]
ai kiểm tra lại hộ cái
Để mình tìm cách ngắn hơn post sau nhé
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
