S
soul92
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
các bác cho hỏi,đê xác định m để h/s đồng biến trên khoảng nào đó,thì yêu cầu cơ bản là phải có điều kiện gì?
làm dùm bài này lun hen:
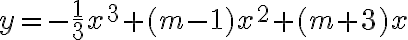 - 4
- 4
xd m để h/s đồng biền trên khoảng 0<x<3
mà nếu trong khoảng (2;5) thì có dk gì khác ko
giúp nhanh dùng nha
làm dùm bài này lun hen:
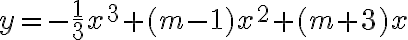
xd m để h/s đồng biền trên khoảng 0<x<3
mà nếu trong khoảng (2;5) thì có dk gì khác ko
giúp nhanh dùng nha
Last edited by a moderator:

