Toán 9 hệ thức lượng trong tam giác vuông

[Nữ Thần Tự Do]

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

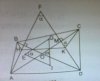
Tứ giác ABCD có các đường chéo cắt nhau ở O và không vuông góc với nhau. Gọi H,K lần lượt là trực tâm của các tam giác AOB và COD. Gọi G,I lần lượt là trọng tâm của các tam giác BOC và AOD.
a) Gọi E là trọng tâm của tam giác AOB, F là giao điểm của AH,DK. Chứng minh rằng các tam giác IEG và HFK đồng dạng
b) Chứng minh rằng IG vuông góc với HK

 

[Khuất Hải Đăng]

chụp mình cái hình vẽ của bạn ok

 

[Nữ Thần Tự Do]

chụp mình cái hình vẽ của bạn ok

Hình đây nha bạn

 

[Khuất Hải Đăng]

a)Gọi góc COD=a (a<90)
có góc IEG= DOC, HFK=DOC
=>IEG= HFK (1)
có EG=1/3 AC; EI=1/3 BD
=> EG / EI= AC/ BD (2)
Gọi M là giao điểm FK và AC
FK= FM+MK= AM*cotg(a)+MC*cotg(a)= AC* cotg(a)
=> FK/FH=AC/BD(3)
(1)(2)(3)=> tam giác IEG đồng dạng tam giác HFK(c.g.c)
b)IE vuông góc HF

 

[Nữ Thần Tự Do]

a)Gọi góc COD=a (a<90)
có góc IEG= DOC, HFK=DOC
=>IEG= HFK (1)
có EG=1/3 AC; EI=1/3 BD
=> EG / EI= AC/ BD (2)
Gọi M là giao điểm FK và AC
FK= FM+MK= AM*cotg(a)+MC*cotg(a)= AC* cotg(a)
=> FK/FH=AC/BD(3)
(1)(2)(3)=> tam giác IEG đồng dạng tam giác HFK(c.g.c)
b)IE vuông góc HF

Cảm ơn bạn nha, nhưng không cần gọi góc COD = a(a<90). Vì góc COD >90 cũng chứng minh IEG=HFK được nha bạn