Cách giải đúng nè mọi người:
Đặt BC=1
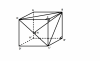
Kẻ BH vuông góc với DC'([tex]H\epsilon DC'[/tex])
Vì ABCD A'B'C'D' là hình hộp chữ nhật nên BC=B'C'=1; BB'=DD'; [tex]\angle BCD=\angle BCC'=\angle BB'C'=\angle CC'D'=90^{O}[/tex]
và DCC'D' là hình chữ nhật (1)
Ta có: [tex]\angle DC'D'+\angle CC'D=90^{O}[/tex] <=> [tex]45^{O}+\angle CC'D=90^{O} => \angle CC'D=45^{O} =>\angle DC'D'=\angle CC'D
=> C'D là tia phân giác của \angle CC'D'[/tex](2)
Từ (1) (2) suy ra DCC'D' là hình vuông => DC=CC'
Xét tam giác BCD và tam giác BCC' có:
[tex]\angle BCD=\angle BCC'=90^{O}; BC chung; DC=CC'(cmt)[/tex]
Suy ra: tam giác BCD= tam giác BCC' (c-g-c) => BD=BC' (2 cạnh tương ứng)
=> tam giác BDC' cân tại B
Mà BH là đường cao của tam giác BDC'
Do đó BH cũng là đường trung tuyến của tam giác BDC'
=>DH=C'H=DC'/2(3)
Aps dụng tỉ số lượng giác của góc nhọn trong tam giác vuông vào tam giác BB'C' vuông tại B' ta có
+) [tex]tan 60^{o}=\frac{BB'}{B'C'}=\frac{BB'}{1}=> BB'=\sqrt{3}=> BB'=DD'=\sqrt{3}[/tex]
+) [tex]cos60^{o}=\frac{B'C'}{BC'}=>\frac{1}{2}=\frac{1}{BC'}=> BC'=2[/tex]
Áp dụng tỉ số lượng giác của góc nhọn trong tam giác vuông vào tam giác DD'C' vuông tại D' ta có
[tex]sin45^{o}=\frac{DD'}{DC'}=> \frac{\sqrt{2}}{2}=\frac{\sqrt{3}}{DC'}=>DC'=\sqrt{6}[/tex] (4)
Từ (3) (4) suy ra DH=C'H=[tex]\frac{\sqrt{6}}{2}[/tex]
Áp dụng tỉ số lượng giác của góc nhọn trong tam giác vuông vào tam giác BC'H vuông tại H ta có
[tex]cos\angle BC'H=\frac{C'H}{BC'}=> [tex]=> cos \angle BC'D=\frac{\frac{\sqrt{6}}{2}}{2}=\frac{\sqrt{6}}{4}=> \angle BC'D\approx 52,2^{O}[/tex]
[/tex]
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
