[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
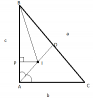
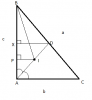
Bài 1: Chứng minh rằng; trong một tam giác vuông ta luôn có :
a, b+c = 2r+2R
b, [tex]\frac{r}{a}\leq (\sqrt{2}-1):2[/tex]
c, 0.4<[tex]\frac{r}{h}<0.5[/tex]
r là bán kính đường tròn nội tiếp
R là bán kính đường tròn ngoại tiếp
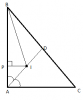
Bài 2: cho tam giác ABC , có trung tuyến CM vuông góc với trung tuyến BN. Chứng minh:
a, cot B + cot C [tex]\geq \frac{2}{3}[/tex]
b, [tex]AB^{2}+AC^{2}=5BC^{2}[/tex]
a, b+c = 2r+2R
b, [tex]\frac{r}{a}\leq (\sqrt{2}-1):2[/tex]
c, 0.4<[tex]\frac{r}{h}<0.5[/tex]
r là bán kính đường tròn nội tiếp
R là bán kính đường tròn ngoại tiếp
Bài 2: cho tam giác ABC , có trung tuyến CM vuông góc với trung tuyến BN. Chứng minh:
a, cot B + cot C [tex]\geq \frac{2}{3}[/tex]
b, [tex]AB^{2}+AC^{2}=5BC^{2}[/tex]