Toán 9 Hệ thức lượng trong tam giác vuông

[ngochaad]

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

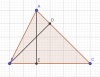
Bài 1: Các cạnh của một tam giác tỉ lệ với 7,8,13.
a, Tính góc lớn nhất
b, Tính diện tích tam giác biết chu vi tam giác là 84 cm


Bài 2: Tính các cạnh của 1 tam giác có 3 đường cao là 12 cm, 15 cm, 20 cm.


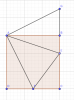
Bài 3: Trên BC , CD của hình vuông ABCD lấy E, F sao cho EC=2EB , FC = FD
Chứng minh [tex]\widehat{AEB}=\widehat{AEF}[/tex]

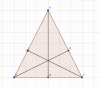
Bài 4: Cho tam giác ABC cân tại A, đường cao AH , BK , CI.
a, Chứng minh [tex]\frac{1}{BK^{2}}=\frac{1}{4AH^{2}}+\frac{1}{BC^{2}}[/tex]
b, chứng minh [tex]3BK^{2}+2AK^{2} +CK^{2} = AB^{2}+BC^{2}+AC^{2}[/tex]

 

[Ann Lee]

Bài 4:

a) $\Delta AHC\sim \Delta BKC(g-g)$
$\Rightarrow \frac{AH}{BK}=\frac{CH}{CK}$
$\Rightarrow AH.CK=CH.BK$
$\Leftrightarrow AH^{2}.CK^{2}=BK^{2}.CH^{2}$
$\Leftrightarrow AH^{2}.(BC^{2}-BK^{2})=BK^{2}.\frac{BC^{2}}{4}$
$\Leftrightarrow AH^{2}.BC^{2}=AH^{2}.BK^{2}+BK^{2}.\frac{BC^{2}}{4}$
Chia cả 2 vế cho $BK^{2}.AH^{2}.BC^{2}$ ta được:
[tex]\frac{1}{BK^{2}}=\frac{1}{4AH^{2}}+\frac{1}{BC^{2}}[/tex] (đpcm)

b) [tex]\Delta BIC=\Delta CKB(ch-gn)\Rightarrow BK=CI;BI=CK\Rightarrow AK=AI[/tex] (vì AB-AC)
Theo định lý pythagores,ta có:

• [tex]AB^{2}=AK^{2}+BK^{2}[/tex]
  
• [tex]AC^{2}=AI^{2}+CI^{2}[/tex]
  
• [tex]CB^{2}=BI^{2}+CI^{2}[/tex]

Suy ra: [tex]AB^{2}+AC^{2}+BC^{2}=AK^{2}+BK^{2}+AI^{2}+CI^{2}+BI^{2}+CI^{2}=3BK^{2}+2AK^{2}+CK^{2}[/tex]

Bài 3:

Hướng làm:
Gọi a là độ dài cạnh của hình vuông ABCD.
Trên tia đối của tia BC láy điểm G sao cho [tex]BG=\frac{a}{2}[/tex]
Có [tex]FC=FD=\frac{a}{2};EC=2EB=\frac{2a}{3}\Rightarrow EB=\frac{a}{3}[/tex]
Đi chứng minh [tex]\Delta AEF=\Delta AEG(c-c-c)[/tex] ( dùng định lý Pythagores để tính độ dài các cạnh EF,EG,AG,AF theo a, chú ý đến các tam giác vuông mà các cạnh này ứng vào).

Bài 2:
Bổ đề 1:
Trong tam giác ABC có 3 cạnh a,b,c và 3 chiều cao $h_{a};h_{b};h_{c}$ tương ứng với 3 cạnh đáy thì [tex]\frac{h_{a}}{h_{b}}=\frac{b}{a};\frac{h_{b}}{h_{c}}=\frac{c}{b};\frac{h_{c}}{h_{a}}=\frac{a}{c}[/tex]


Chứng minh bổ đề :
Gọi tam giác ABC có 3 cạnh BC=a; AC=b; AB=c. Chiều cao tương ứng là ha,hb,hc.
[tex]S_{ABC}=\frac{1}{2}AE.BC=\frac{1}{2}BD.AC\Rightarrow AE.BC=BD.AC\Leftrightarrow \frac{AE}{BD}=\frac{AC}{BC}\Leftrightarrow \frac{h_{a}}{h_{b}}=\frac{b}{a} [/tex] (đpcm)
Chứng minh tương tự.....

Bổ đề 2:
Một tam giác có cạnh a,b,c là tam giác vuông nếu các chiều cao $h_{a};h_{b};h_{c}$ tương ứng của nó thỏa mãn điều kiện: [tex](\frac{h_{a}}{h_{b}})^{2}+(\frac{h_{a}}{h_{c}})^{2}=1[/tex]
Chứng minh bổ đề 2:
Áp dụng bổ đề 1, ta được:
[tex](\frac{h_{a}}{h_{b}})^{2}+(\frac{h_{a}}{h_{c}})^{2}=1\Leftrightarrow (\frac{b}{a})^{2}+(\frac{c}{a})^{2}=1\Rightarrow a^{2}=b^{2}+c^{2}[/tex]
=> Tam giác đã cho là tam giác vuông (đpcm)
______________________________________
Gọi độ dài 3 cạnh của tam giác ứng với 3 đường cao là 12 cm, 15 cm, 20 cm lần lượt là a,b,c
Áp dụng bổ đề 2 ta được:
$(\frac{12}{15})^{2}+(\frac{12}{20})^{2}=1$
Suy ra tam giác này là tam giác vuông có 2 cạnh góc vuông là 15cm và 20cm
=> còn còn lại là cạnh huyền và có độ dài là 25 cm