[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Lý thuyết Một số phương trình lượng giác cơ bản
1. Phương trình bậc nhất đối với một hàm số lượng giác
Các phương trình dạng at + b = 0 (a≠ 0), với t là một trong các hàm số lượng giác được gọi là phương trình bậc nhất đối với một hàm số lượng giác.
Từ phương trình trên ta tính được t = - b/a và được phương trình lượng giác cơ bản đã xét trong bài 2.
Bằng cách sử dụng các phép biến đổi lượng giác, ta có thể đưa nhiều phương trình lượng giác về phương trình bậc nhất đối với một hàm số lượng giác.
2. Phương trình bậc nhất đối với sinx và cosx
Xét phương trình asinx + bcosx = c (1) với a, b là các số thực khác 0.
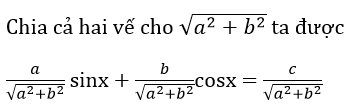
Khi đó phương trình (1) được đưa về dạng
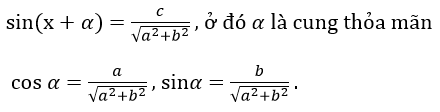
3. Phương trình bậc hai đối với một hàm số lượng giác
Các phương trình dạng at2 + bt + c = 0 (a≠ 0), với t là một trong các hàm số lượng giác được gọi là phương trình bậc hai đối với một hàm số lượng giác.
Giải phương trình trên ta tính được t, từ đó đưa về việc giải một phương trình lượng giác cơ bản.
Bằng cách sử dụng các phép biến đổi lượng giác, ta có thể đưa nhiều phương trình lượng giác về phương trình bậc hai đối với một hàm số lượng giác.
1. Phương trình bậc nhất đối với một hàm số lượng giác
Các phương trình dạng at + b = 0 (a≠ 0), với t là một trong các hàm số lượng giác được gọi là phương trình bậc nhất đối với một hàm số lượng giác.
Từ phương trình trên ta tính được t = - b/a và được phương trình lượng giác cơ bản đã xét trong bài 2.
Bằng cách sử dụng các phép biến đổi lượng giác, ta có thể đưa nhiều phương trình lượng giác về phương trình bậc nhất đối với một hàm số lượng giác.
2. Phương trình bậc nhất đối với sinx và cosx
Xét phương trình asinx + bcosx = c (1) với a, b là các số thực khác 0.
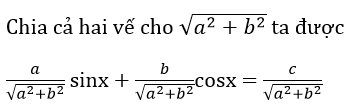
Khi đó phương trình (1) được đưa về dạng
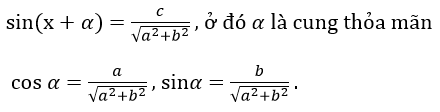
3. Phương trình bậc hai đối với một hàm số lượng giác
Các phương trình dạng at2 + bt + c = 0 (a≠ 0), với t là một trong các hàm số lượng giác được gọi là phương trình bậc hai đối với một hàm số lượng giác.
Giải phương trình trên ta tính được t, từ đó đưa về việc giải một phương trình lượng giác cơ bản.
Bằng cách sử dụng các phép biến đổi lượng giác, ta có thể đưa nhiều phương trình lượng giác về phương trình bậc hai đối với một hàm số lượng giác.