Giúp mình bài này nha.
Cho y = x^(2) - 3x + 2 (P)
a) Lập bảng biến thiên và vẽ đồ thị
b) Dựa vào (P), chỉ ra điều kiện của x để y=0 , y > 0, y < 0
TXĐ : D = R
Đỉnh: ( [tex]\frac{3}{2}[/tex] ; [tex]\frac{-1}{4}[/tex]
=> Trục đối xứng là [tex]\frac{3}{2}[/tex]
Bảng biến thiên:
Mình không có điện thoại nên không chụp được bảng, sorry bạn nhiều nha. Bạn vẽ theo cái này:
A là [tex]-\infty[/tex]
B là [tex]\frac{3}{2}[/tex]
C là [tex]+\infty[/tex]
D là [tex]\frac{-1}{4}[/tex]
Y và E là [tex]-\infty[/tex]
Giao điểm với trục hoành thì tung độ bằng 0
y=0 =>
[tex]x^2-3x+2[/tex] =0
<=> x= 2 => A1(2;0)
và x=1 => A2(1;0)
Giao điểm với trục tung thì hoànhđộ bằng 0
x=0 => y=2 => A3(0;2)
Đồ thị
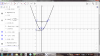
Mình vẽ không được đẹp thông cảm nha.
A3d là điểm đối xứng của A3 qua trục đối xứng nha.
b, Dựa vào P ta có
[tex]x^2-3x+2[/tex] =0
=> x= 2 ; x=1
[tex]x^2-3x+2[/tex] >0
=> [tex]x^2-3.2x.\frac{3}{2}+\frac{9}{4}-\frac{9}{4}+2[/tex] >0
=>
[tex](x-\frac{3}{2})^2-\frac{1}{4} >0[/tex]
=> x nằm trong khoảng.
( [tex]-\infty[/tex] ; 1) [tex]\cup[/tex] ( 2; [tex]+\infty[/tex] ) /
/ [tex]x^2-3x+2[/tex] >0 /
=>
[tex](x-\frac{3}{2})^2-\frac{1}{4} <0[/tex]
=> x nằm trong khoảng
(1;2)
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
