- 27 Tháng mười 2018
- 3,742
- 3,706
- 561
- Hà Nội
- Trường Đại học Bách Khoa Hà Nội
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Hai đồ thị tiếp xúc nhau tại 1 điểm nào đó. Mô tả về mặt đồ thị sẽ như sau:
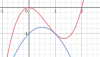
Chúng ta có thể thấy 2 đồ thị này tiếp xúc nhau tại điểm có hoành độ x=1.
Vậy cách làm sẽ như sau:
Cách 1:
Cho 2 đồ thị (c):f(x) và (d) : g(x). 2 đồ thị này tiếp xúc nhau tại 1 điểm M nếu hoành độ của M thỏa mãn hệ điều kiện sau:
[tex]\left\{\begin{matrix} f(x)=g(x)\\ f'(x)=g'(x) \end{matrix}\right.[/tex]
Nói cách khác, M chính là tiếp điểm của tiếp tuyến chung của (c) và (d).
Cách 2: 2 đồ thị tiếp xúc tại 1 điểm, thì hoành độ điểm đó chính là nghiệm bội chẵn của pt hoành độ giao điểm của 2 đồ thị. Vậy ta chỉ cần giải pt và tìm nghiệm bội chẵn là được.
Vận dụng:
1. Tìm điểm tiếp xúc ( nếu có ) của 2 đồ thị hàm số sau: f(x)=[TEX]-3x^2+4x+4[/TEX] và g(x)=[TEX]-x^2+8x+6[/TEX]
Giải: Ta xét hệ :
[tex]\left\{\begin{matrix} f(x)=g(x)\\ f'(x)=g'(x) \end{matrix}\right. <=>\left\{\begin{matrix} -3x^2+4x+4=-x^2+8x+6\\ -6x+4=-2x+8 \end{matrix}\right. <=>\left\{\begin{matrix} x^2+2x+1=0\\ 4x=4 \end{matrix}\right. <=>x=1[/tex]
Vậy tiếp điểm của 2 đồ thị hàm f(x) và g(x) là điểm A(1;5)
2. Cho hàm số: [tex]f(x)=\frac{x^2-3x+3}{x-2}[/tex] có đồ thị (c), và đường thẳng (d):y=-3x+m.
Định m để đồ thị (c) tiếp xúc với (d).
Giải:
Cách 1: Xét hệ pt :
[tex]\left\{\begin{matrix} \frac{x^2-3x+3}{x-2}=-3x+m\\ \frac{x^2-4x+3}{(x-2)^2}=-3 \end{matrix}\right. <=>\left\{\begin{matrix} \frac{x^2-3x+3}{x-2}=-3x+m\\ 4x^2-16x+15 \end{matrix}\right. <=>\left\{\begin{matrix} \frac{x^2-3x+3}{x-2}=-3x+m\\ x=1,5;x=2,5 \end{matrix}\right.[/tex]
Do hệ trên phải có nghiệm nên thay từng giá trị x đã tìm được ở pt 2 vào pt 1 ta sẽ tìm được m.
Với x=1,5 =>m=3
Với x=2,5=>m=11
Vậy có 2 giá trị thỏa mãn của m là m=3 hoặc m=11.
Cách 2: Xét pt hoành độ giao điểm của (c) và (d):
[tex]\frac{x^2-3x+3}{x-2}=-3x+m<=>4x^2-(m+9)x+3+2m=0(1)[/tex]
Pt (1) ở bên trên cần phải có nghiệm kép, tức [TEX]\delta[/TEX] = 0
<=>[tex](m+9)^2-16(3+2m)=0<=>m^2-14m+33=0<=>m=11;m=3[/tex]
Kết quả hoàn toàn giống.
Nhận xét: Với bài toán mà pt hoành độ giao điểm chỉ là pt bậc 2 thì nên áp dụng cách 2 để biện luận, sẽ nhanh hơn. Còn với pt bậc cao hơn 2, thì để biện luận ta nên dùng cách 1.
3. Tìm k để hai đồ thị sau tiếp xúc với nhau: [TEX]f(x)=x^3-3x+1,g(x)=k(x-1)-1[/TEX]
Đáp án: k=0, k=-9/4
4. Tìm m để 2 đồ thị sau tiếp xúc với nhau: [TEX]f(x)=x^2-4x+m,g(x)=x^3-3x^2+1[/TEX]
Đáp án: m=1, m=59/27
Chúng ta có thể thấy 2 đồ thị này tiếp xúc nhau tại điểm có hoành độ x=1.
Vậy cách làm sẽ như sau:
Cách 1:
Cho 2 đồ thị (c):f(x) và (d) : g(x). 2 đồ thị này tiếp xúc nhau tại 1 điểm M nếu hoành độ của M thỏa mãn hệ điều kiện sau:
[tex]\left\{\begin{matrix} f(x)=g(x)\\ f'(x)=g'(x) \end{matrix}\right.[/tex]
Nói cách khác, M chính là tiếp điểm của tiếp tuyến chung của (c) và (d).
Cách 2: 2 đồ thị tiếp xúc tại 1 điểm, thì hoành độ điểm đó chính là nghiệm bội chẵn của pt hoành độ giao điểm của 2 đồ thị. Vậy ta chỉ cần giải pt và tìm nghiệm bội chẵn là được.
Vận dụng:
1. Tìm điểm tiếp xúc ( nếu có ) của 2 đồ thị hàm số sau: f(x)=[TEX]-3x^2+4x+4[/TEX] và g(x)=[TEX]-x^2+8x+6[/TEX]
Giải: Ta xét hệ :
[tex]\left\{\begin{matrix} f(x)=g(x)\\ f'(x)=g'(x) \end{matrix}\right. <=>\left\{\begin{matrix} -3x^2+4x+4=-x^2+8x+6\\ -6x+4=-2x+8 \end{matrix}\right. <=>\left\{\begin{matrix} x^2+2x+1=0\\ 4x=4 \end{matrix}\right. <=>x=1[/tex]
Vậy tiếp điểm của 2 đồ thị hàm f(x) và g(x) là điểm A(1;5)
2. Cho hàm số: [tex]f(x)=\frac{x^2-3x+3}{x-2}[/tex] có đồ thị (c), và đường thẳng (d):y=-3x+m.
Định m để đồ thị (c) tiếp xúc với (d).
Giải:
Cách 1: Xét hệ pt :
[tex]\left\{\begin{matrix} \frac{x^2-3x+3}{x-2}=-3x+m\\ \frac{x^2-4x+3}{(x-2)^2}=-3 \end{matrix}\right. <=>\left\{\begin{matrix} \frac{x^2-3x+3}{x-2}=-3x+m\\ 4x^2-16x+15 \end{matrix}\right. <=>\left\{\begin{matrix} \frac{x^2-3x+3}{x-2}=-3x+m\\ x=1,5;x=2,5 \end{matrix}\right.[/tex]
Do hệ trên phải có nghiệm nên thay từng giá trị x đã tìm được ở pt 2 vào pt 1 ta sẽ tìm được m.
Với x=1,5 =>m=3
Với x=2,5=>m=11
Vậy có 2 giá trị thỏa mãn của m là m=3 hoặc m=11.
Cách 2: Xét pt hoành độ giao điểm của (c) và (d):
[tex]\frac{x^2-3x+3}{x-2}=-3x+m<=>4x^2-(m+9)x+3+2m=0(1)[/tex]
Pt (1) ở bên trên cần phải có nghiệm kép, tức [TEX]\delta[/TEX] = 0
<=>[tex](m+9)^2-16(3+2m)=0<=>m^2-14m+33=0<=>m=11;m=3[/tex]
Kết quả hoàn toàn giống.
Nhận xét: Với bài toán mà pt hoành độ giao điểm chỉ là pt bậc 2 thì nên áp dụng cách 2 để biện luận, sẽ nhanh hơn. Còn với pt bậc cao hơn 2, thì để biện luận ta nên dùng cách 1.
3. Tìm k để hai đồ thị sau tiếp xúc với nhau: [TEX]f(x)=x^3-3x+1,g(x)=k(x-1)-1[/TEX]
Đáp án: k=0, k=-9/4
4. Tìm m để 2 đồ thị sau tiếp xúc với nhau: [TEX]f(x)=x^2-4x+m,g(x)=x^3-3x^2+1[/TEX]
Đáp án: m=1, m=59/27
