- 24 Tháng mười 2018
- 1,616
- 1,346
- 216
- 24
- TP Hồ Chí Minh
- Đại học Sư phạm Kỹ thuật TP Hồ Chí Minh
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
1. GTLN và GTNN của hàm đơn điệu
xét [tex]y=f(x)[/tex] trên đoạn [a;b].
- nếu f(x) đồng biến trên đoạn [a;b] thì [tex]minf(x)=f(a)[/tex] và [tex]maxf(x)=f(b)[/tex]
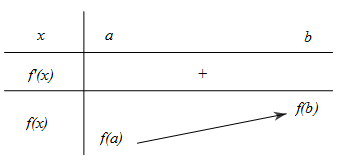
- nếu f(x) nghịch biến biến trên đoạn [a;b] thì [tex]minf(x)=f(b)[/tex] và [tex]maxf(x)=f(a)[/tex]
* chú ý:
- hàm số [tex]y=f(x)[/tex] là hàm đồng biến trên khoảng (a;b) nếu [tex]f'(x)\geq 0,\forall x\in (a;b)[/tex] và dấu "=" xảy ra tại hữu hạn điểm.
- hàm số [tex]y=f(x)[/tex] là hàm nghịch biến trên khoảng (a;b) nếu [tex]f'(x)\leq 0,\forall x\in (a;b)[/tex] và dấu "=" xảy ra tại hữu hạn điểm.
2. ví dụ minh họa
ví dụ 1: tìm m để [tex]y=\frac{2x-m^2-m}{x+1}[/tex] có GTNN trên đoạn [0;1] là -6.
giải:
[tex]y'=\frac{m^2+m+2}{(x+1)^2}> 0,\forall x\in [0;1][/tex]
do đó hàm số [tex]y=\frac{2x-m^2-m}{x+1}[/tex] đồng biến trên đoạn [0;1]
nên GTNN trên đoạn [0;1] là [tex]miny=f(0)[/tex].
ta có: [tex]f(0)=-6<=>\frac{-m^2-m}{1}=-6<=>m^2+m-6=0<=>m=-3\vee m=2[/tex]
ví dụ 2: tìm m để [tex]y=\frac{x+m}{x+1}[/tex] có [tex]\underset{[1;2]}{miny}+\underset{[1;2]}{maxy}=\frac{16}{3}[/tex]
giải:
[tex]y'=\frac{1-m}{(x+1)^2}[/tex]
- xét với [tex]m=1=>y=1[/tex]. hàm số là hàm hằng nên [tex]miny=maxy=1[/tex] (loại).
- với [tex]m\neq 1[/tex] thì hàm số đơn điệu trên [1;2].
nếu hàm đồng biến thì [tex]miny=f(1); maxy=f(2)[/tex]. nếu hàm nghịch biến thì [tex]miny=f(2);maxy=f(1)[/tex]
do đó, ta nhận xét rằng dù đồng biến hay nghịch biến thì tổng [tex]miny+maxy=f(1)+f(2)[/tex]
vậy, [tex]f(1)+f(2)=\frac{16}{3}<=>\frac{1+m}{2}+\frac{2+m}{3}=\frac{16}{3}<=>m=5[/tex]
vậy, m=5.
ví dụ 3: tìm m để [tex]y=\frac{x+m}{x-1}[/tex] có [tex]\underset{[2;4]}{miny}=3[/tex].
giải: [tex]y'=\frac{-1-m}{(x-1)^2}[/tex]
- xét với [tex]-1-m=0<=>m=-1=>y=1[/tex] (loại).
xét với [tex]-1-m<0<=>m>-1[/tex], hàm nghịch biến. suy ra [tex]miny=f(4)<=>f(4)=3<=>\frac{4+m}{3}=3<=>m=5[/tex]
xét với [tex]-1-m>0<=>m<-1[/tex], hàm đồng biến. suy ra [tex]miny=f(2)<=>f(2)=3<=>\frac{2+m}{1}=3<=>m=1[/tex] (loại)
vậy giá trị thỏa mãn duy nhất là m=5.
xét [tex]y=f(x)[/tex] trên đoạn [a;b].
- nếu f(x) đồng biến trên đoạn [a;b] thì [tex]minf(x)=f(a)[/tex] và [tex]maxf(x)=f(b)[/tex]
- nếu f(x) nghịch biến biến trên đoạn [a;b] thì [tex]minf(x)=f(b)[/tex] và [tex]maxf(x)=f(a)[/tex]
* chú ý:
- hàm số [tex]y=f(x)[/tex] là hàm đồng biến trên khoảng (a;b) nếu [tex]f'(x)\geq 0,\forall x\in (a;b)[/tex] và dấu "=" xảy ra tại hữu hạn điểm.
- hàm số [tex]y=f(x)[/tex] là hàm nghịch biến trên khoảng (a;b) nếu [tex]f'(x)\leq 0,\forall x\in (a;b)[/tex] và dấu "=" xảy ra tại hữu hạn điểm.
2. ví dụ minh họa
ví dụ 1: tìm m để [tex]y=\frac{2x-m^2-m}{x+1}[/tex] có GTNN trên đoạn [0;1] là -6.
giải:
[tex]y'=\frac{m^2+m+2}{(x+1)^2}> 0,\forall x\in [0;1][/tex]
do đó hàm số [tex]y=\frac{2x-m^2-m}{x+1}[/tex] đồng biến trên đoạn [0;1]
nên GTNN trên đoạn [0;1] là [tex]miny=f(0)[/tex].
ta có: [tex]f(0)=-6<=>\frac{-m^2-m}{1}=-6<=>m^2+m-6=0<=>m=-3\vee m=2[/tex]
ví dụ 2: tìm m để [tex]y=\frac{x+m}{x+1}[/tex] có [tex]\underset{[1;2]}{miny}+\underset{[1;2]}{maxy}=\frac{16}{3}[/tex]
giải:
[tex]y'=\frac{1-m}{(x+1)^2}[/tex]
- xét với [tex]m=1=>y=1[/tex]. hàm số là hàm hằng nên [tex]miny=maxy=1[/tex] (loại).
- với [tex]m\neq 1[/tex] thì hàm số đơn điệu trên [1;2].
nếu hàm đồng biến thì [tex]miny=f(1); maxy=f(2)[/tex]. nếu hàm nghịch biến thì [tex]miny=f(2);maxy=f(1)[/tex]
do đó, ta nhận xét rằng dù đồng biến hay nghịch biến thì tổng [tex]miny+maxy=f(1)+f(2)[/tex]
vậy, [tex]f(1)+f(2)=\frac{16}{3}<=>\frac{1+m}{2}+\frac{2+m}{3}=\frac{16}{3}<=>m=5[/tex]
vậy, m=5.
ví dụ 3: tìm m để [tex]y=\frac{x+m}{x-1}[/tex] có [tex]\underset{[2;4]}{miny}=3[/tex].
giải: [tex]y'=\frac{-1-m}{(x-1)^2}[/tex]
- xét với [tex]-1-m=0<=>m=-1=>y=1[/tex] (loại).
xét với [tex]-1-m<0<=>m>-1[/tex], hàm nghịch biến. suy ra [tex]miny=f(4)<=>f(4)=3<=>\frac{4+m}{3}=3<=>m=5[/tex]
xét với [tex]-1-m>0<=>m<-1[/tex], hàm đồng biến. suy ra [tex]miny=f(2)<=>f(2)=3<=>\frac{2+m}{1}=3<=>m=1[/tex] (loại)
vậy giá trị thỏa mãn duy nhất là m=5.
