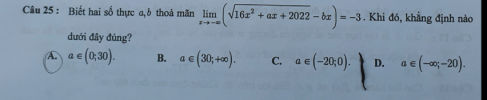[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Biết 2 số thực [imath]a,b[/imath] thỏa mãn [imath]\lim _{x \to -\infty} (\sqrt{16x^2+ax+2022}-bx)=-3[/imath]. Khẳng định nào dưới đây đúng"
A. [imath]a \in (0,30)[/imath]
B. [imath]a \in (30,+\infty)[/imath]
C. [imath]a \in (-20,0)[/imath]
D. [imath]a \in (-\infty,-20)[/imath]
A. [imath]a \in (0,30)[/imath]
B. [imath]a \in (30,+\infty)[/imath]
C. [imath]a \in (-20,0)[/imath]
D. [imath]a \in (-\infty,-20)[/imath]
Attachments
Last edited by a moderator: